
[2012·湖南卷] 如图1-7,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(1)证明:BD⊥PC;
(2)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
解:(1)证明:因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD.
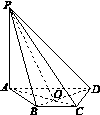
图1-8
又AC⊥BD,PA,AC是平面PAC内的两条相交直线,所以BD⊥平面PAC.
而PC⊂平面PAC,所以BD⊥PC.
(2)设AC和BD相交于点O,连结PO,由(1)知,BD⊥平面PAC,所以∠DPO是直线PD和平面PAC所成的角.从而∠DPO=30°.
由BD⊥平面PAC,PO⊂平面PAC知,BD⊥PO.
在Rt△POD中,由∠DPO=30°得PD=2OD.
因为四边形ABCD为等腰梯形,AC⊥BD,所以△AOD,△BOC均为等腰直角三角形.从而梯形ABCD的高为![]() AD+
AD+![]() BC=
BC=![]() ×(4+2)=3,于是梯形ABCD的面积S=
×(4+2)=3,于是梯形ABCD的面积S=![]() ×(4+2)×3=9.
×(4+2)×3=9.
在等腰直角三角形AOD中,OD=![]() AD=2
AD=2![]() ,所以PD=2OD=4
,所以PD=2OD=4![]() ,PA=
,PA=![]() =4.
=4.
故四棱锥P-ABCD的体积为
V=![]() ×S×PA=
×S×PA=![]() ×9×4=12.
×9×4=12.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(2012年高考湖南卷理科5)已知双曲线C :![]() -
-![]() =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
A.![]() -
-![]() =1 B.
=1 B.![]() -
-![]() =1 C.
=1 C.![]() -
-![]() =1 D.
=1 D.![]() -
-![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
[2012·湖南卷] 如图1-7,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(1)证明:BD⊥PC;
(2)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考湖南卷理科21)(本小题满分13分)
在直角坐标系xOy中,曲线C1的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=﹣2的距离等于该点与圆C2上点的距离的最小值.
(Ⅰ)求曲线C1的方程;
(Ⅱ)设P(x0,y0)(y0≠±3)为圆C2外一点,过P作圆C2的两条切线,分别与曲线C1相交于点A,B和C,D.证明:当P在直线x=﹣4上运动时,四点A,B,C,D的纵坐标之积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com