
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.
科目:高中数学 来源: 题型:
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定
正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]() ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为![]() ,求
,求![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]() ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为![]() ,求
,求![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市花都区高三调研考试理科数学卷 题型:解答题
(本题满分12分)某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要
回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是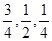 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为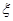 ,求
,求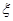 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分)
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是![]() ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为![]() ,求
,求![]() 的分布列、数学期望和方差.
的分布列、数学期望和方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com