

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 根据程序框图的流程,计算运行n次的结果,根据输入$a=\frac{10}{21}$,判断n满足的条件,从而求出输出的k值.
解答 解:由程序框图知第一次运行s=0+$\frac{1}{1×3}$,k=2;
第二次运行s=0+$\frac{1}{1×3}$+$\frac{1}{3×5}$,k=3;
…
∴第n次运行s=0+$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$×(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
当输入a=$\frac{10}{21}$时,由S>a得n>10,程序运行了11次,输出的k值为12.
故选:D.
点评 本题考查了直到型循环结构的程序框图,由程序框图判断程序运行的功能,用裂项相消法求和是解答本题的关键,属于基础题.


 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
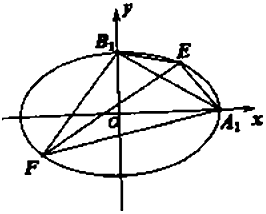 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过 点A1,B1引椭圆C的两条弦A1E、B1F.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率是$\frac{\sqrt{3}}{2}$,且过点($\sqrt{3}$,$\frac{1}{2}$).设点A1,B1分别是椭圆的右顶点和上顶点,如图所示过 点A1,B1引椭圆C的两条弦A1E、B1F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com