
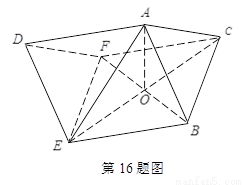
在棱长为2的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,AB=AE,连结AO.

(Ⅰ)求证:AO⊥平面FEBC;
(Ⅱ)求二面角B-AC-E的大小.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
 16、在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO
16、在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO查看答案和解析>>
科目:高中数学 来源:山东肥城六中2008届高中数学(新课标)模拟示范卷4 题型:044
(理)在棱长为2的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,AB=AE,连结AO.
(Ⅰ)求证:AO⊥平面FEBC;
(Ⅱ)求二面角B-AC-E的余弦值的大小;
(Ⅲ)求三棱锥B-DEF的体积.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省南通市通州区高三4月查漏补缺专项检测数学试卷(解析版) 题型:解答题
在所有棱长都相等的斜三棱柱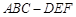 中,已知
中,已知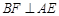 ,
,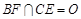 ,且
,且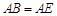 ,连接
,连接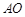 .
.
(1)求证: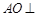 平面
平面 ;
;
(2)求证:四边形 为正方形.
为正方形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO
在所有棱长都相等的斜三棱柱ABC-DEF中,已知BF⊥AE,BF∩CE=O,且AB=AE,连接AO查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com