
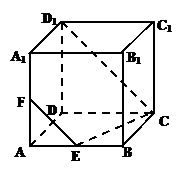
在正方体
 中,E为AB中点,F为
中,E为AB中点,F为 的中点.
的中点.
求证:
(1)E、C、 、F四点共面;
、F四点共面;
(2)CE
、 、DA三线共点.
、DA三线共点.
|
证明: (1)如图所示,连结EF、 、 、 . .
∵ E、F分别是AB和 的中点, 的中点,
∴ EF∥ 且 且 . .
又∵  , ,
∴四边形  是平行四边形. 是平行四边形.
∴  .从而EF∥ .从而EF∥ . .
由推论 3,EF与 确定一个平面. 确定一个平面.
∴ E、F、 、C四点共面. 、C四点共面.
(2) ∵E为AB的中点,∴ . .
又 AB∥DC,∴AE∥DC且 . .
∴延长 CE,则CE与DA必相交,设其交点为H,∴有 DA∩CE=H,如图所示.
∵EC ∴H∈平面 同理,DA ∴H∈平面 ∴点H在平面 易证平面 ∴H∈直线 ∴CE, |
|
要证CE, |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
如图所示,在正方体![]() 中,E为AB的中点
中,E为AB的中点
(1)若![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() ∥面
∥面![]() ;
;
(2) 若![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值;
的余弦值;
(3)若![]() 在
在![]() 上运动时(
上运动时(![]() 与
与![]() 、
、![]() 不重合),
不重合),
求当半平面![]() 与半平面
与半平面![]() 成
成![]() 的角时,线段
的角时,线段![]() 的比.
的比.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三第一次月考数学理卷 题型:解答题
(本小题满分12分)如图所示,在正方体 中,
中,
E为AB的中点
(1)若 为
为 的中点,求证:
的中点,求证: 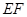 ∥面
∥面 ;
;
(2) 若 为
为 的中点,求二面角
的中点,求二面角 的余弦值;
的余弦值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com