
分析 分别画出y=|x2-2x|与y=a(x+1)的图象,则存在两个整数,使得y=|x2-2x|在直线y=ax+a的下方,结合图象即可求出函数a的范围
解答  解:f(x)=|x2-2x|-ax-a<0,
解:f(x)=|x2-2x|-ax-a<0,
则|x2-2x|<ax+a,
分别画出y=|x2-2x|与y=a(x+1)的图象,如图所示,
∵只存在两个整数x,使得f(x)<0,
当x=1时,y=|12-2|=1,
∴2a=1,
解得a=$\frac{1}{2}$,此时有2个整数,
结合图象可得a的取值范围为(0,$\frac{1}{2}$],
故答案为(0,$\frac{1}{2}$].
点评 本题分段函数的问题,涉及数形结合和转化的思想,属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
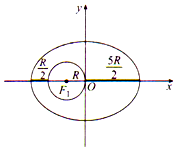 我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )
我国自主研制的第一个月球探测器--“嫦娥一号”卫星在西昌卫星发射中心成功发射后,在地球轨道上经历3次调相轨道变轨,奔向月球,进入月球轨道,“嫦娥一号”轨道是以地心为一个焦点的椭圆,设地球半径为R,卫星近地点,远地点离地面的距离分别是$\frac{R}{2}$,$\frac{5R}{2}$(如图所示),则“嫦娥一号”卫星轨道的离心率为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| f(x) | 2 | 0 | 3 | 1 |
| x | 0 | 1 | 2 | 3 |
| g(x) | 2 | 1 | 0 | 3 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
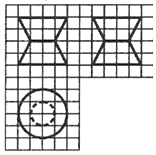 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com