
| 支持 | 无所谓 | 反对 | |
| 高一年级 | 18 | x | 2 |
| 高二年级 | 10 | 6 | y |
| 高一年级 | 高二年级 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 (1)(i)由题可得x=5,y=4;
(ii)利用列举法确定基本事件,即可求恰好高一、高二各1人的概率;
(2)根据表格统计的数据,完成下面的2×2的列联表,求出K2,与临界值比较,即可判断是否有90%的把握认为持支持与就读年级有关.
解答 解:(1)( i)由题可得x=5,y=4.
( ii)假设高一反对的编号为A1,A2,高二反对的编号为B1,B2,B3,B4,
则选取两人的所有结果为:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),(A2,B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4).
∴恰好高一、高二各一人包含8个事件,
∴所求概率$p=\frac{8}{15}$.
(2)如图列联表:
| 高一年级 | 高二年级 | 总计 | |
| 支持 | 18 | 10 | 28 |
| 不支持 | 7 | 10 | 17 |
| 总计 | 25 | 20 | 45 |
点评 本题考查概率的计算,考查独立性检验知识的运用,考查学生分析解决问题的能力,属于中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x<4} | B. | {x|x≤4} | C. | {x|1≤x<4} | D. | {x|1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
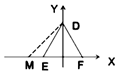 如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )
如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )| A. | 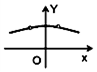 | B. | 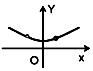 | C. | 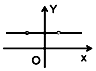 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
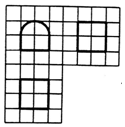 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )| A. | 10+2π | B. | 12+3π | C. | 20+4π | D. | 16+5π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com