练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    一条河两岸平行，河的宽度d=500 m，一艘船从A处出发到河对岸.已知船的速度|v1|=10 km/h,水流速度|v2|=2 km/h,问行驶航程最短时，所用时间是多少（精确到0.1 min）？

    解析：要使航程最短，需使船的速度与水流速度的合速度v必须垂直于对岸.

    如图知：|v|=(km/h),

    所以t=×60≈3.1(min),

    即行驶航程最短时，所用时间是3.1 min.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

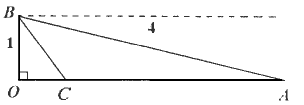
    如下图，一条河宽1km，相距4km(直线距离)的两座城市，A，B分别位于河的两岸(假定岸是平行的直线)，现需铺设一条电缆连通A与B，已知地下电缆的修建费为每千米2万元，水下电缆的修建费为每千米4万元，问应如何铺设电缆可使总的修建费用最少？(＝1.732，＝2.236，＝3.8730)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

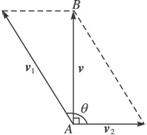
    一条河的两岸平行,河的宽度为d.一艘船以速度v1航行,水流速度为v2(|v2|＜|v1|),船的实际行驶速度为v,当船最快到达对岸时,应（    ）

    A.v1⊥v2                          B.v与v2夹角为45°

    C.v1⊥v                            D.v2⊥v

    查看答案和解析>>

    科目：高中数学 来源： 题型：

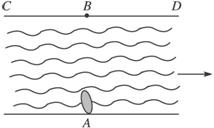
    如图(1)（2）,一条河的两岸平行,河的宽度d=500 m.一艘船从A处出发到河对岸.已知船的速度|v1|=10 km/h,水流速度|v2|=2 km/h,问行驶航程最短时,所用时间是多少(精确到0.1 min)?

                

    图（1）                                                                        图（2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图,一条河的两岸平行,河的宽度d=500 m.一艘船从A出发航行到河对岸,船航行的速度|v1|=10 km/h,水流速度|v2|=4 km/h,设v1和v2的夹角为θ(0＜θ＜π).

    (1)当θ多大时,船能垂直到达对岸(即船的实际速度v=v1+v2与河岸垂直)?(精确到1°,可利用计算器计算)

    (2)当船垂直到达对岸时,航行所需时间最少吗?为什么?

    查看答案和解析>>

    同步练习册答案