
解析:要写出参数方程,首先根据直线的普通方程可以看出直线的斜率为2,设直线的倾斜角为α,则tanα=2,则sinα=![]() ,cosα=
,cosα=![]() ,根据后边要求的点M恰好在直线上,为了后边的运算方便,选择M作为直线上的定点.要求点M到A、B的距离可以根据参数方程的特点及几何意义或者两点之间的距离公式都可以.
,根据后边要求的点M恰好在直线上,为了后边的运算方便,选择M作为直线上的定点.要求点M到A、B的距离可以根据参数方程的特点及几何意义或者两点之间的距离公式都可以.
解:根据直线的普通方程可知斜率是2,设直线的倾斜角为α,?
则tanα=2,sinα=![]() ,cosα=
,cosα=![]() ,?
,?
所以直线的参数方程是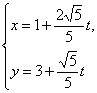 (t为参数).?
(t为参数).?
经验证易知点A(3,7)恰好在直线上,所以有1+![]() t=3,即t=5,即点M到点A的距离是5.?
t=3,即t=5,即点M到点A的距离是5.?
而点B(8,6)不在直线上,所以不能使用参数t的几何意义,可以根据两点之间的距离公式求出距离为![]()
点评:本题主要考查直线参数方程的转化和参数的几何意义.常见错误:①转化参数方程时不注意后边的题目内容,随便取一个定点;②把点B(8,6)当成直线上的点很容易由1+![]() t=8,得t=
t=8,得t=![]() .
.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com