
(1)x∈[0,π];
(2)x∈[-2π,4π];
(3)x∈R.
思路分析:记住arccosx∈[0,π],利用诱导公式或利用终边相同的三角函数相等可求解.
解:(1)由余弦函数在闭区间[0,π]上是减函数和cosx=-![]() 知:符合条件的角有且只有一个,这个角为钝角.
知:符合条件的角有且只有一个,这个角为钝角.
设cosθ=![]() ,θ∈(0,
,θ∈(0,![]() ),由反余弦定义可知:
),由反余弦定义可知:
θ=arccos![]() .
.
∵![]() <π-θ<π,
<π-θ<π,
且cos(π-θ)=-cosθ=-![]() =cosx.
=cosx.
∴x=π-θ=π-arccos![]() .
.
(2)∵x∈[-2π,4π],由余弦函数的图象及周期性可知:在长度为6π的区间上,满足cosx=-![]() 的角x有6个.
的角x有6个.
设cosθ=-![]() ,θ∈(0,
,θ∈(0, ![]() ),由定义知:θ=arccos
),由定义知:θ=arccos![]() ;
;
由cosx=-![]() <0知角x的终边在第二或第三象限,由诱导公式可知在[0,2π]内:符合cosx=-
<0知角x的终边在第二或第三象限,由诱导公式可知在[0,2π]内:符合cosx=-![]() 的角x=π-θ和π+θ.
的角x=π-θ和π+θ.
即x1=π-arccos![]() ,x2=π+arccos
,x2=π+arccos![]() ;从而在[2π,4π]内符合条件的角x3=x1+2π=3π-arccos
;从而在[2π,4π]内符合条件的角x3=x1+2π=3π-arccos![]() ,x4=x2+2π=3π+arccos
,x4=x2+2π=3π+arccos![]() ;在[-2π,0]内符合条件的角x5=x1-2π=-π-arccos
;在[-2π,0]内符合条件的角x5=x1-2π=-π-arccos![]() ,x6=x2-2π=-π+arccos
,x6=x2-2π=-π+arccos![]() ,即在[-2π,4π]内,满足cosx=-
,即在[-2π,4π]内,满足cosx=-![]() 的角x的集合为{π±arccos
的角x的集合为{π±arccos![]() ,3π±arccos
,3π±arccos![]() ,-π±arccos
,-π±arccos![]() }.
}.
(3)∵x是任意角,∴满足cosx=-![]() 的角x有无穷多个,它的终边在第二或第三象限,由定义知:在[0,2π]内符合条件的角x1=π-arccos
的角x有无穷多个,它的终边在第二或第三象限,由定义知:在[0,2π]内符合条件的角x1=π-arccos![]() 和x2=π+arccos
和x2=π+arccos![]() ,由终边相同的角的集合的表达式可知:符合cosx=-
,由终边相同的角的集合的表达式可知:符合cosx=-![]() 的所有的角x的集合为{x|x=2kπ+π±arccos
的所有的角x的集合为{x|x=2kπ+π±arccos![]() ,k∈Z}.
,k∈Z}.


科目:高中数学 来源:2012年山东省临沂市高考数学二模试卷(理科)(解析版) 题型:解答题
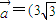 cosx,
cosx,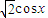 ),
),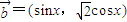 ,设函数f(x)=
,设函数f(x)=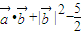 .
. ]时,求函数f(x)的值域;
]时,求函数f(x)的值域;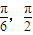 ]且f(α)=
]且f(α)=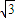 ,求f(
,求f(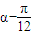 )的值.
)的值.查看答案和解析>>
科目:高中数学 来源:2011年山东省济南市平阴县高考数学模拟试卷(文科)(解析版) 题型:解答题
 cosx),
cosx), =(cosx,cosx),f(x)=
=(cosx,cosx),f(x)= .
. ,求x的取值集合;(2)求函数f(x)的周期及增区间.
,求x的取值集合;(2)求函数f(x)的周期及增区间.查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三会考模拟试卷数学 题型:解答题
( 7分)
已知 = (cosx,sinx),
= (cosx,sinx), = (-cosx,cosx),函数f (x)=
= (-cosx,cosx),函数f (x)=  .
.
(Ⅰ)求函数f (x)的最小正周期;
(Ⅱ) 当x∈ 时,求f(x)的值域.
时,求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com