
 其中c>0,那么f(x)的零点是________.
其中c>0,那么f(x)的零点是________.科目:高中数学 来源:2012-2013学年浙江省嘉兴市高三(上)基础测试数学试卷(理科)(解析版) 题型:选择题
 其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)-
其中[x]表示不超过x的最大整数,如[-1.3]=-2,[1.3]=1,则函数y=f(x)- x-
x- 不同零点的个数( )
不同零点的个数( )查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波市余姚中学高三(上)第一次质量检测数学试卷(实验班)(解析版) 题型:解答题
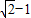 函数f(x)=
函数f(x)= 其中
其中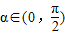
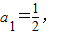 an+1=f(an)(n∈N*)求证:
an+1=f(an)(n∈N*)求证: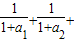 …+
…+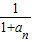 <2(n≥2,n∈N*).
<2(n≥2,n∈N*).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
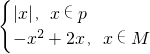 其中P,M是非空数集,且P∩M=φ,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.
其中P,M是非空数集,且P∩M=φ,设f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.查看答案和解析>>
科目:高中数学 来源: 题型:
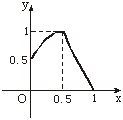
其中f1(x)=-2(x-![]() )2+1,f2(x)=-2x+2.
)2+1,f2(x)=-2x+2.
(Ⅰ)在下面坐标系上画出y=f(x)的图象;
(Ⅱ)设y=f2(x)(x![]() [
[![]() ])的反函数为y=g(x),a1=1,a2=g(a1),…,an=g(an-1);
])的反函数为y=g(x),a1=1,a2=g(a1),…,an=g(an-1);
求数列{an}的通项公式,并求![]() ;
;
(Ⅲ)若x0![]() [0,
[0,![]() ),x1=f(x0),f(x1)=x0,求x0.
),x1=f(x0),f(x1)=x0,求x0.
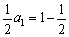
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省无锡市宜兴市丁蜀高级中学高三数学限时训练(1)(解析版) 题型:填空题
 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断其中正确的序号为 :
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断其中正确的序号为 :查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com