
(1)求![]() 在区间[t,t+1]上的最大值h(t);
在区间[t,t+1]上的最大值h(t);
(2)是否存在实数m,使得![]() 的图象与
的图象与![]() 的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由.
的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由.
解:(1)![]() =-x2+8x=-(x-4)2+16.
=-x2+8x=-(x-4)2+16.
当t+1<4,即t<3时, ![]() 在[t,t+1]上单调递增,
在[t,t+1]上单调递增,
![]() ;
;
当t≤4≤t+1,即3≤t≤4时,h(t)=f(4)=16;
当t>4时, ![]() 在[t,t+1]上单调递减,
在[t,t+1]上单调递减,
![]() =-t2+8t.
=-t2+8t.
综上,h(t)=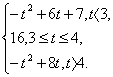
(2)函数![]() 的图象与
的图象与![]() 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点,
即函数φ(x)=![]() -
-![]() 的图象与x轴的正半轴有且只有三个不同的交点.
的图象与x轴的正半轴有且只有三个不同的交点.
∵φ(x)=x2-8x+6lnx+m,
∴φ′(x)=2x-8+![]() =
=![]() =
=![]() ,
,
当x∈(0,1)时,φ′(x)>0,φ(x)是增函数;
当x∈(1,3)时,φ′(x)<0,φ(x)是减函数;
当x∈(3,+∞)时,φ′(x)>0,φ(x)是增函数;
当x=1或x=3时,φ′(x)=0.
∴φ(x)max=φ(1)=m-7,
φ(x)min=φ(3)=m+6ln3-15.
∵当x充分接近0时,φ(x)<0;当x充分大时,φ(x)>0.
∴要使φ(x)的图象与x轴正半轴有三个不同的交点,必须且只需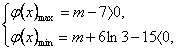
即7<m<15-6ln3.
∴存在实数m,使得函数![]() 与
与![]() 的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3).
的图象有且只有三个不同的交点,m的取值范围为(7,15-6ln3).


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
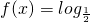 [x2-2(2a-1)x+8](a∈R)
[x2-2(2a-1)x+8](a∈R) 时,求y=f(
时,求y=f( ),x∈[
),x∈[ ]的值域.
]的值域. 在[1,3]上有且只有一解,求a的取值范围.
在[1,3]上有且只有一解,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省南昌二中高一(上)第二次月考数学试卷(解析版) 题型:解答题
 [x2-2(2a-1)x+8](a∈R)
[x2-2(2a-1)x+8](a∈R) 时,求y=f(
时,求y=f( ),x∈[
),x∈[ ]的值域.
]的值域. 在[1,3]上有且只有一解,求a的取值范围.
在[1,3]上有且只有一解,求a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com