
分析 (1)求出f(x)的导数,求出单调区间,可得极小值且为最小值,无最大值;
(2)当a<0时,f′(x)=1-$\frac{a}{x}$>0在x∈[4,5]上恒成立,可得函数f(x)在x∈[4,5]上单调递增.利用g′(x)>0在x∈[4,5]上恒成立,可得g(x)在x∈[4,5]上为增函数.不妨设x2>x1,则|f(x1)-f(x2)|<|g(x1)-g(x2)|恒成立|恒成立?f(x2)-f(x1)<g(x2)-g(x1)恒成立,即f(x2)-g(x2)<f(x1)-g(x1)在x∈[4,5]上恒成立.设F(x)=f(x)-g(x)=x-alnx-1-$\frac{{e}^{x}}{x}$.则F(x)在x∈[4,5]上为减函数.分离参数利用导数进一步研究即可得出.
解答 解:(1)当a=$\frac{1}{e}$时,函数f(x)=x-1-$\frac{1}{e}$lnx(x>0),
导数为f′(x)=1-$\frac{1}{ex}$=$\frac{ex-1}{ex}$,
当x>$\frac{1}{e}$时,f′(x)>0,f(x)递增;当0<x<$\frac{1}{e}$时,f′(x)<0,f(x)递减.
可得f(x)在x=$\frac{1}{e}$处f(x)取得极小值,且为最小值$\frac{1}{e}$-1+1=$\frac{1}{e}$,无最大值;
(2)当a<0时,f′(x)=1-$\frac{a}{x}$>0在x∈[4,5]上恒成立,
∴函数f(x)在x∈[4,5]上单调递增,
g(x)=$\frac{{e}^{x}}{x}$,
∵g′(x)=$\frac{{e}^{x}(x-1)}{{x}^{2}}$>0在x∈[4,5]上恒成立,
∴g(x)在[4,5]上为增函数.
当a<0时,且对任意的x1,x2∈[4,5](x1≠x2),|f(x1)-f(x2)|<|g(x1)-g(x2)|恒成立,
即f(x2)-g(x2)<f(x1)-g(x1)在x∈[4,5]上恒成立.
设F(x)=f(x)-g(x)=x-alnx-1-$\frac{{e}^{x}}{x}$.则F(x)在x∈[4,5]上为减函数.
F′(x)=1-$\frac{a}{x}$-$\frac{{e}^{x}(x-1)}{{x}^{2}}$≤0在x∈[4,5]上恒成立,化为a≥x-ex+$\frac{{e}^{x}}{x}$恒成立.
设H(x)=x-ex+$\frac{{e}^{x}}{x}$,
∵H′(x)=1-ex+$\frac{{e}^{x}(x-1)}{{x}^{2}}$=1-ex(1-$\frac{1}{x}$+$\frac{1}{{x}^{2}}$)=1-ex[($\frac{1}{x}$-$\frac{1}{2}$)2+$\frac{3}{4}$],x∈[4,5].
∴ex[($\frac{1}{x}$-$\frac{1}{2}$)2+$\frac{3}{4}$]>$\frac{3}{4}$e3>1,x∈[4,5].
∴H′(x)<0在x∈[4,5]上恒成立,即H(x)为减函数.
∴H(x)在x∈[4,5]上的最大值为H(4)=4-e4+$\frac{1}{4}$e4=4-$\frac{3}{4}$e4.
∴4-$\frac{3}{4}$e4≤a<0.
点评 本题考查了利用函数导数研究函数的单调性、极值与最值,考查了恒成立问题的等价转化方法,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,±4) | B. | (±4,4) | C. | (±$\frac{79}{16}$,$\frac{\sqrt{79}}{8}$) | D. | (±$\frac{\sqrt{79}}{8}$,$\frac{79}{16}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
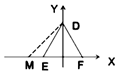 如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )
如图所示,△DEF中,已知DE=DF,点M在直线EF上从左到右运动(点M不与E、F重合),对于M的每一个位置(x,0),记△DEM的外接圆面积与△DMF的外接圆面积的比值为f(x),那么函数y=f(x)的大致图象为( )| A. | 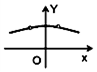 | B. | 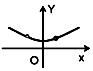 | C. | 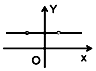 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2014,+∞) | B. | (0,2014) | C. | (0,2020) | D. | (2020,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
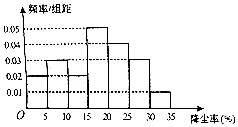 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com