
如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.

(1)若![]() =
=![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
 如图所示,M,N是函数y=2sin(wx+φ)(ω>0)图象与x轴的交点,
如图所示,M,N是函数y=2sin(wx+φ)(ω>0)图象与x轴的交点,| PM |
| PN |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•宁德模拟)已知函数f(x)=2sin(ωx+φ)(ω>0,丨φ丨<
(2013•宁德模拟)已知函数f(x)=2sin(ωx+φ)(ω>0,丨φ丨<| π |
| 2 |
| 7 |
| ||
| 14 |
查看答案和解析>>
科目:高中数学 来源:高考总复习全解 数学 一轮复习·必修课程 (人教实验版) B版 人教实验版 B版 题型:047
如图所示,M,N,P,Q分别是正方体ABCD-![]() 中棱AB,BC,
中棱AB,BC,![]() ,C
,C![]() 的中点.
的中点.
求证:M,N,P,Q四点共面.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,M、N、P分别是正方体ABCD-A1B1C1D1的棱AB、BC、DD1上的点.
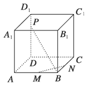
(1)若![]() =
=![]() ,求证:无论点P在DD1上如何移动,总有BP⊥MN;
,求证:无论点P在DD1上如何移动,总有BP⊥MN;
(2)棱DD1上是否存在这样的点P,使得平面APC1⊥平面ACC1?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com