
设![]() =(-2,2,5)、
=(-2,2,5)、![]() =(6,-4,4)分别是平面α,β的法向量,则平面α,β的位置关系是
=(6,-4,4)分别是平面α,β的法向量,则平面α,β的位置关系是
平行
垂直
相交但不垂直
不能确定
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:江西省重点中学2009年三月新课标高一月考试卷 数学 题型:044
如果有穷数列a1,a2,a3,…am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次出{bn}的每一项;
(2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;
(3)设{dn}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列.
求{dn}前n项的和Sn(n=1,2,…,100).
查看答案和解析>>
科目:高中数学 来源:2007年普通高等学校招生全国统一考试、文科数学(上海卷) 题型:044
如果有穷数列a1,a2,a3,…,am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.
例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项;
(2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;
(3)设{dn}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列.求{dn}前n项的和Sn(n=1,2,…,100).
查看答案和解析>>
科目:高中数学 来源:2012年普通高等学校招生全国统一考试上海卷数学文科 题型:044
对于项数为m的有穷数列{an},记bk=max{a1,a2,…,ak}(k=1,2,…,m),即bk为a1,a2,…,ak中的最大值,并称数列{bn}是{an}的控制数列,如1,3,2,5,5的控制数列是1,3,3,5,5.
(1)若各项均为正整数的数列{an}的控制数列为2,3,4,5,5,写出所有的{an};
(2)设{bn}是{an}的控制数列,满足ak=bm-k+1=C(C为常数,k=1,2,…,m),求证:bk=ak(k=1,2,…,m);
(3)设m=100,常数a∈(![]() ,1),若an=an2-(-1)
,1),若an=an2-(-1)![]() n,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
n,{bn}是{an}的控制数列,求(b1-a1)+(b2-a2)+…+(b100-a100).
查看答案和解析>>
科目:高中数学 来源: 题型:
(A) {1,2} (B) (3,4,5} (C) {1,2,6,7} (D) {1,2,3,4,5}
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省武威市高一下学期期中测试数学试卷(解析版) 题型:解答题
设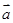 =(-1,1),
=(-1,1),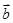 =(x,3),
=(x,3),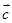 =(5,y),
=(5,y),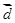 =(8,6),且
=(8,6),且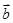 ∥
∥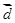 ,(4
,(4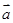 +
+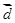 )⊥
)⊥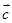 .
.
(1)求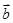 和
和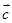 ;
;
(2)求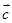 在
在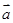 方向上的射影;
方向上的射影;
(3)求λ1和λ2,使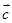 =λ1
=λ1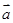 +λ2
+λ2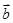 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com