
思路分析:在直角坐标系中,求曲线的轨迹方程的方法有直接法、定义法、转移法,在极坐标系中,求曲线的极坐标方程这几种方法仍然是适用的.
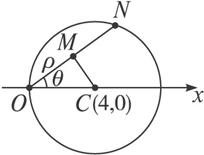
图1-3-3
解:如图1-3-3,圆C的圆心C(4,0),半径r=|OC|=4,连结CM.
∵M为弦ON的中点,
∴CM⊥ON,故M在以OC为直径的圆上.
∴动点M的轨迹方程是ρ=4cosθ.
方法归纳 这种解法是定义法,下面我们用转移法来解决这个问题:设M点的坐标是(ρ,θ),N(ρ1,θ1).N点在圆ρ=8cosθ上,
∴ρ1=8cosθ1(*).∵M是ON的中点,∴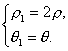 它代入(*)式得2ρ=8cosθ.故M的轨迹方程是ρ=4cosθ.
它代入(*)式得2ρ=8cosθ.故M的轨迹方程是ρ=4cosθ.
在极坐标系中,曲线可以用含有ρ,θ这两个变数的方程f(ρ,θ)来表示,这种方程叫做曲线的极坐标方程.常见的曲线方程如下:
①过极点,极角为α的直线方程:θ=α(ρ∈R).
②与极轴平行并且与极轴距离等于a的直线方程:ρsinθ=±a(a>0).
③与极轴所在直线垂直且与极点距离为a的直线方程:ρcosθ=±a(a>0).
④圆的极坐标方程:
圆心为(ρ0,θ0),半径为r:ρ2-2ρ0-ρcos(θ-θ0)+ρ02-r2=0;
圆心为(ρ0,0),半径为r:ρ2-2ρ0ρcosθ+ρ02-r2=0;
圆心为(r,0),半径为r:ρ=2rcosθ(r>0);
圆心为(-r,0),半径为r:ρ=-2rcosθ(r>0);
圆心为(r,![]() ),半径为r:ρ=2rsinθ(r>0);
),半径为r:ρ=2rsinθ(r>0);
圆心为(r,![]() ),半径为r:ρ=-2rsinθ(r>0);
),半径为r:ρ=-2rsinθ(r>0);
圆心为(0,θ),半径为r:ρ=r(r>0).


科目:高中数学 来源: 题型:
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.1 1 |
| 2 |
| π |
| 4 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com