练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知菱形OABC，
    OA
    =
    a
    ，
    OC
    =
    c
    ，
    a
    =（2，1），＜
    a
    ，
    c
    ＞=
    π
    3
    ，则菱形的面积为
    5
    		3
    2
    5
    		3
    2
    ．
    分析：由题意可知，|
    a
    |=|
    c
    |    =
    		5
    ，∠AOC=
    1
    3
    π    ，菱形的面积S=2S△AOC，结合三角形的面积公式可求
    解答：解：由题意可知，|
    a
    |=|
    c
    |    =
    		5
    ，∠AOC=
    1
    3
    π
    ∴菱形的面积S=2S△AOC=2×
    1
    2
    ×
    		5
    ×
    		5
    ×
    		3
    2
    =
    5
    		3
    2

    故答案为
    5
    		3
    2
    点评：本题主要考查了向量的夹角定义的简单应用及 三角形的面积公式的应用，试题比较容易
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C的左、右焦点分别是F1、F2，离心率为
    		3
    2
    ，过F1且垂直于x轴的直线被椭圆C截得的线段长为1；
    （Ⅰ）求椭圆C的方程．
    （Ⅱ）若A，B，C是椭圆上的三个点，O是坐标原点，当点B是椭圆C的右顶点，且四边形OABC为菱形时，求此菱形的面积．
    （Ⅲ）设点p是椭圆C上除长轴端点外的任一点，连接PF1、PF2，设∠F1PF2的角平分线PM交椭圆C的长轴于点M（m，0），求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•北京）已知A，B，C是椭圆W：
    x24
    +y2=1    上的三个点，O是坐标原点．
    （Ⅰ）当点B是W的右顶点，且四边形OABC为菱形时，求此菱形的面积；
    （Ⅱ）当点B不是W的顶点时，判断四边形OABC是否可能为菱形，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年上海交大附中高三数学理总复习二推理与证明等练习卷（解析版） 题型：解答题

    已知A，B，C是椭圆W：＋y2＝1上的三个点，O是坐标原点．

    (1)当点B是W的右顶点，且四边形OABC为菱形时，求此菱形的面积；

    (2)当点B不是W的顶点时，判断四边形OABC是否可能为菱形，并说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届新课标版高三上学期第四次月考理科数学试卷（解析版） 题型：解答题

    已知A、B、C是椭圆W: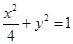上的三个点,O是坐标原点.

    (I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积；

    (II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由。

     

    查看答案和解析>>

    科目：高中数学 来源：2013年全国普通高等学校招生统一考试理科数学（北京卷解析版） 题型：解答题

    已知A、B、C是椭圆W：上的三个点，O是坐标原点.

    (I)当点B是W的右顶点，且四边形OABC为菱形时，求此菱形的面积.

    (II)当点B不是W的顶点时，判断四边形OABC是否可能为菱形，并说明理由.

     

    查看答案和解析>>

    同步练习册答案