
分析 (1)f′(x)=2ax+1-2a-$\frac{1}{x}$=$\frac{(2ax+1)(x-1)}{x}$.(x∈[1,2]).对a分类讨论,利用导数研究函数的单调性极值与最值,即可得出.
(2)f′(x)=2ax+1-2a-$\frac{1}{x}$,f′(x0)=a(x1+x2)+1-2a-$\frac{2}{{x}_{1}+{x}_{2}}$.而$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$=a(x1+x2)+(1-2a)+$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{1}-{x}_{2}}$.
作差可得f′(x0)-$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$=-$\frac{2}{{x}_{1}+{x}_{2}}$-$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{1}-{x}_{2}}$=$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-$\frac{2}{{x}_{1}+{x}_{2}}$.不妨设0<x1<x2,令$\frac{{x}_{2}}{{x}_{1}}=t>1$.由$ln\frac{{x}_{2}}{{x}_{1}}$-$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$=$ln\frac{{x}_{2}}{{x}_{1}}$-$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{\frac{{x}_{2}}{{x}_{1}}+1}$=lnt-$\frac{2(t-1)}{t+1}$=g(t),t>1.利用导数研究其单调性极值与最值即可得出.
解答 解:(1)f′(x)=2ax+1-2a-$\frac{1}{x}$=$\frac{(2ax+1)(x-1)}{x}$.(x∈[1,2]).
①a=0,f′(x)=$\frac{x-1}{x}$,可得f′(x)≥0,∴函数f(x)在x∈[1,2]上单调递增,因此x=2时,函数f(x)取得最大值,
f(2)=2-ln2.
②a≠0时,f′(x)=$\frac{2a(x-\frac{1}{-2a})(x-1)}{x}$.
a>0时,可得f′(x)≥0,∴函数f(x)在x∈[1,2]上单调递增,因此x=2时,函数f(x)取得最大值,f(2)=2-ln2.
$-\frac{1}{4}<a<0$时,$\frac{1}{-2a}$>2,可得f′(x)≥0,∴函数f(x)在x∈[1,2]上单调递增,因此x=2时,函数f(x)取得最大值,f(2)=2-ln2.
$a=-\frac{1}{4}$时,f′(x)=$\frac{-(x-2)(x-1)}{2x}$,可得f′(x)≥0,∴函数f(x)在x∈[1,2]上单调递增,因此x=2时,函数f(x)取得最大值,f(2)=2-ln2.
$-\frac{1}{2}<a<-\frac{1}{4}$时,2>$\frac{1}{-2a}$>1.可得x=-$\frac{1}{2a}$时,函数f(x)取得最大值,f(-$\frac{1}{2a}$)=1-$\frac{1}{4a}$+ln(-2a).
$a=-\frac{1}{2}$时,f′(x)=$\frac{-(x-1)^{2}}{x}$≤0,∴函数f(x)在x∈[1,2]上单调递减,因此x=1时,函数f(x)取得最大值,
f(1)=1-a.
a$<-\frac{1}{2}$时,0<$\frac{1}{-2a}$<1,可得f′(x)≤0,∴函数f(x)在x∈[1,2]上单调递减,因此x=1时,函数f(x)取得最大值,f(1)=1-a.
综上可得:$a≥-\frac{1}{4}$时,函数f(x)取得最大值为f(2)=2-ln2.
$-\frac{1}{2}≤a<-\frac{1}{4}$时,函数f(x)取得最大值f(-$\frac{1}{2a}$)=1-$\frac{1}{4a}$+ln(-2a).
a$<-\frac{1}{2}$时,函数f(x)取得最大值,f(1)=1-a.
(2)f′(x)=2ax+1-2a-$\frac{1}{x}$,f′(x0)=a(x1+x2)+1-2a-$\frac{2}{{x}_{1}+{x}_{2}}$.
y1-y2=$a{x}_{1}^{2}$+(1-2a)x1-lnx1-[a${x}_{2}^{2}$+(1-2a)x2-lnx2]=a(x1+x2)(x1-x2)+(1-2a)(x1-x2)+ln$\frac{{x}_{2}}{{x}_{1}}$.
∴$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$=a(x1+x2)+(1-2a)+$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{1}-{x}_{2}}$.
∴f′(x0)-$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$=-$\frac{2}{{x}_{1}+{x}_{2}}$-$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{1}-{x}_{2}}$=$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-$\frac{2}{{x}_{1}+{x}_{2}}$.
不妨设0<x1<x2,令$\frac{{x}_{2}}{{x}_{1}}=t>1$.
由$ln\frac{{x}_{2}}{{x}_{1}}$-$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$=$ln\frac{{x}_{2}}{{x}_{1}}$-$\frac{2(\frac{{x}_{2}}{{x}_{1}}-1)}{\frac{{x}_{2}}{{x}_{1}}+1}$=lnt-$\frac{2(t-1)}{t+1}$=g(t),t>1.
则g′(t)=$\frac{1}{t}$-$\frac{4}{(t+1)^{2}}$=$\frac{(t-1)^{2}}{t(t+1)^{2}}$>0,
∴函数g(t)在(1,+∞)上单调递增.
∴g(t)>g(1)=0.
∴$ln\frac{{x}_{2}}{{x}_{1}}$-$\frac{2({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}$>0,
∴$\frac{ln\frac{{x}_{2}}{{x}_{1}}}{{x}_{2}-{x}_{1}}$-$\frac{2}{{x}_{1}+{x}_{2}}$>0.
∴f′(x0)>$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$.
点评 本题考查了利用导数研究其单调性极值与最值、作差法、换元法、方程与不等式的解法、分类讨论方法,考查了推理能力与计算能力,属于难题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,使得x02-x0+2=0 | |
| B. | 命题“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 在△ABC中,“A=B”是“sinA=sinB”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [-$\frac{π}{6}$,$\frac{5π}{6}$] | D. | [$\frac{π}{6}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
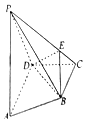 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2,在侧面PAD中,PA=PD,E为侧棱PC上不同于端点的任意一点且PA⊥DE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
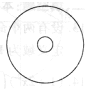 如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
如图,半径为5cm的圆形纸板内有一个相同圆心的半径为1cm的小圆,现将半径为1cm的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{21}{25}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{55}$ | B. | $\frac{1}{58}$ | C. | $\frac{1}{61}$ | D. | $\frac{1}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com