Question

斜率为2的直线l被双曲线截得的弦长为4，求直线l的方程．

Answer 1

【答案】分析：先设出直线l的方程，利用弦长公式求出弦长，让弦长等于4，即可求出参数的值．
解答：解：设直线l的方程为y=2x+m，与双曲线交于A，B两点．
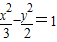
设A，B两点的坐标分别为A（x₁，y₁），B（x₂，y₂），将y=2x+m代入并整理得：
10x²+12mx+3+3（m²+2）=0，
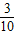
∴x₁+x₂=-m，x₁x₂=（m²+2）
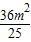
∴（x₁-x₂）²=（x₁+x₂）²-4x₁x₂=-（m²+2）
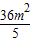
∴|AB|²=（1+k²）（x₁-x₂）²=5（x₁-x₂）²=-6（m²+2）=16，
解得：m=±
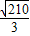
∴所求直线的方程为：y=2x±
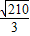点评：本题主要考察了弦长公式的应用，属于圆锥曲线的常规题．