
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
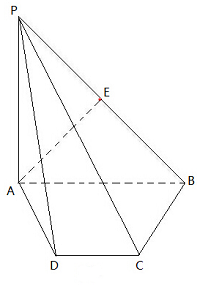 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA⊥底面ABCD,E为PB中点,PA=a.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA⊥底面ABCD,E为PB中点,PA=a.| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
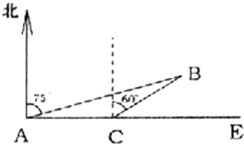 2008年2月26日,中国海军三艘舰艇从海南省三亚启航赴亚丁湾、索马里海域执行首次护航任务,是我国15世纪后最大远征.参与此次护航任务的舰艇有169“武汉”号导弹驱逐舰、171“海口”号导弹驱逐舰、887“微山湖”号综合补给舰.假设护航编队在索马里海域执行护航任务时(如图),海中有一小岛,周围3.8海里内有暗礁.军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°.若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?
2008年2月26日,中国海军三艘舰艇从海南省三亚启航赴亚丁湾、索马里海域执行首次护航任务,是我国15世纪后最大远征.参与此次护航任务的舰艇有169“武汉”号导弹驱逐舰、171“海口”号导弹驱逐舰、887“微山湖”号综合补给舰.假设护航编队在索马里海域执行护航任务时(如图),海中有一小岛,周围3.8海里内有暗礁.军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°.若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?查看答案和解析>>
科目:高中数学 来源: 题型:
| y1 | y2 | 总计 | |
| x1 | a | 21 | 73 |
| x2 | 8 | 25 | 33 |
| 总计 | b | 46 |
| A、94 96 |
| B、52 50 |
| C、52 60 |
| D、54 52 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com