
已知关于 的函数
的函数
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若函数 没有零点,求实数
没有零点,求实数 取值范围.
取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)先求导再讨论其单调性,根据单调性可求其极值。(Ⅱ)先求导再讨论函数的单调性,根据单调性求其极值或最值,因为函数没有零点,所以函数的极大值小于0或极小值大于0。否则函数将存在零点。
试题解析:解:(Ⅰ) ,
, .
2分
.
2分
当 时,
时, ,
, 的情况如下表:
的情况如下表:

所以,当 时,函数
时,函数 的极小值为
的极小值为 .
6分
.
6分
(Ⅱ) .
.
①当 时,
时, 的情况如下表:
的情况如下表:

7分
因为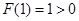 ,
8分
,
8分
若使函数 没有零点,需且仅需
没有零点,需且仅需 ,解得
,解得 ,
9分
,
9分
所以此时 ;
10分
;
10分
②当 时,
时, 的情况如下表:
的情况如下表:
 11分
11分
因为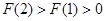 ,且
,且 ,
12分
,
12分
所以此时函数 总存在零点.
13分
总存在零点.
13分
综上所述,所求实数 的取值范围是
的取值范围是 .
.
考点:考查导数和利用导数研究函数性质的方法的数学思想,意在考查考生灵活应用导数分析、解决问题的能力,考查考生的逻辑思维能力、运算能力和创新应用能力。


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源:2011-2012学年陕西省西安市高三第二次月考理科数学试卷 题型:选择题
已知关于 的函数
的函数 ,若点
,若点 是区域
是区域
内任意一点,则函数 在
在 上有零点的概率为(
)
上有零点的概率为(
)
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三期末模拟考试理科数学试卷(四) 题型:选择题
已知关于 的函数
的函数 ,若点
,若点 是区域
是区域
内任意一点,则函数 在
在 上有零点的概率为( )
上有零点的概率为( )
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com