考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据三角函数的图象和性质即可求周期,振幅,单调区间,对称轴,对称中心;
(2)根据三角函数图象之间的关系即可得到结论;
(3)作出一个周期内的图象;
(4)将方程f(x)-lgx=0转化为f(x)=lgx,利用数形结合即可得到结论.
解答:
解:(1)∵函数f(x)=sin(2x+
),
∴周期T=
=π,振幅为1,
由2kπ-
≤2x+
≤2kπ
+,
解得kπ-
≤x≤kπ+
,k∈Z,即函数的递增区间为[kπ-
,kπ+
],k∈Z,
由2kπ+
≤2x+
≤2kπ+
,
解得kπ+
≤x≤kπ+
,k∈Z,即函数的递减区间为[kπ+
,kπ+
],k∈Z,
由2x+
=kπ
+,解得x=
+
,即函数的对称轴为x=
+
,
由2x+
=kπ,解得x=
-
,即函数的对称中心为(
-
,0);
(2)将y=sinx的图象沿着x轴向左平移
个单位得到y=sin(x+
),然后纵坐标不变横坐标表位原来的
,即可得到f(x)=sin(2x+
)的图象;
(3)函数在一个周期内的图象;

(4)由f(x)-lgx=0得f(x)=lgx,
作出f(x)和y=lgx的图象可知,两个图象6个交点,
即方程由6个根.

点评:本题主要考查三角函数的图象和性质,要求熟练掌握相应的公式.





 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
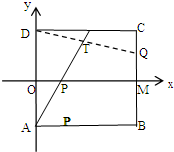 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为