
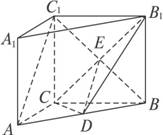
图2-1
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
思路分析:本题考查平行,垂直的论证及异面直线所成角的求法.要充分分析题目中的平行,垂直条件,可以用立体几何的方法来证,也可以用向量法来证.
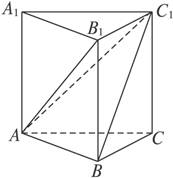
证明:方法一:(1)∵直三棱柱ABC—A1B1C1底面三边长AC=3,BC=4,AB=5,
∴AC⊥BC,且BC1在平面ABC内的射影为BC,
∴AC⊥BC1.

(2)如图,设CB1与C1B的交点为E,连结DE,
∵D是AB的中点,E是BC1的中点,
∴DE∥AC1.
∵DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,
平面CDB1,
∴AC1∥平面CDB1.
(3)∵DE∥AC1,
∴∠CED为AC1与B1C所成的角.
在△CED中,ED=![]() AC1=
AC1=![]() ,CD=
,CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=
CB1=![]() ,
,
∴cos∠CED=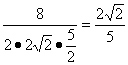 .
.
∴异面直线AC1与B1C所成角的余弦值为![]() .
.
方法二:∵直三棱柱ABC—A1B1C1底面三边长AC=3,BC=4,AB=5,
∴AC,BC,C1C两两垂直.
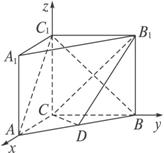
如图,以C为坐标原点,分别以直线CA,CB,CC1为x轴,y轴,z轴,建立空间直角坐标系,
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),D(![]() ,2,0).
,2,0).
(1)∵![]() =(-3,0,0),BC1=(0,-4,4),
=(-3,0,0),BC1=(0,-4,4),
∴![]() ·
·![]() =0.∴AC⊥BC1.
=0.∴AC⊥BC1.
(2)设CB1与C1B的交点为E,则E(0,2,2).
∵![]() =(
=(![]() ,0,2),
,0,2),![]() =(-3,0,4),∴
=(-3,0,4),∴![]() =
=![]()
![]() .∴DE∥AC1.
.∴DE∥AC1.
又∵![]()
![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,∴AC1∥平面CDB1.
平面CDB1,∴AC1∥平面CDB1.
(3)∵![]() =(-3,0,4),
=(-3,0,4),![]() =(0,4,4),
=(0,4,4),
∴cos〈![]() ,
,![]() 〉=
〉=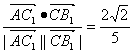 .
.
∴异面直线AC1与B1C所成角的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
如图3,在直三棱柱ABC—A1B1C1中,AB1⊥BC1,AB=CC1=1,BC=2.
(1)求证:A1C1⊥AB;
(2)求点B1到平面ABC1的距离.
查看答案和解析>>
科目:高中数学 来源:2011届湖北省黄冈中学高三5月模拟考试文科数学 题型:解答题
(本小题满分12分)
如图2,在直三棱柱ABC- 中,AB=1,
中,AB=1, ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com