
分析 (Ⅰ)由题意,a=2,c=$\sqrt{3}$,b=1,即可求椭圆C的方程;
(Ⅱ)直线l的方程为x=my-$\sqrt{3}$,与椭圆方程联立,消去x得:(m2+4)y2-2$\sqrt{3}$my-1=0,利用弦长公式、一元二次方程的根与系数的关系,即可得出结论.
解答 解:(Ⅰ)由题意,a=2,c=$\sqrt{3}$,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(Ⅱ)F(-$\sqrt{3}$,0),设A(x1,y1),B(x2,y2),直线l的方程为x=my-$\sqrt{3}$,
与椭圆方程联立,消去x得:(m2+4)y2-2$\sqrt{3}$my-1=0,
y1+y2=$\frac{2\sqrt{3}m}{{m}^{2}+4}$,y1y2=-$\frac{1}{{m}^{2}+4}$,
∴|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\frac{4({m}^{2}+1)}{{m}^{2}+4}$,
∵|AF||BF|=|y1y2|(1+m2)=$\frac{1+{m}^{2}}{{m}^{2}+4}$,
∴|AB|=4|AF||BF|,
∴存在常数λ=4,使|AB|=λ|AF||BF|恒成立.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、弦长公式、一元二次方程的根与系数的关系,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 视觉 听觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | b | |
| 偏高 | 2 | a | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
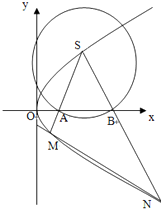 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com