
 已知函数f(x)=|x+1|-|x-3|.
已知函数f(x)=|x+1|-|x-3|.分析 (Ⅰ)运用绝对值的含义,对x讨论,分x>3,-1≤x≤3,x<-1,去掉绝对值,画出图象即可;
(Ⅱ)运用绝对值不等式的性质,可得不等式右边的最大值为2,再由不等式恒成立思想可得f(x)≥2,再由去绝对值的方法,即可解得x的范围.
解答  解:(Ⅰ)由零点分段法,
解:(Ⅰ)由零点分段法,
得f(x)=$\left\{\begin{array}{l}{-4,x<-1}\\{2x-2.-1≤x≤3}\\{4,x>3}\end{array}\right.$,
函数f(x)的图象如图所示:
(Ⅱ)$\frac{|3m+1|-|1-m|}{|m+1|}$≤$\frac{|3m+1+1-m|}{|m+1|}$=2,
当且仅当(3m+1)(1-m)≤0,
且|3m+1|≥|1-m|,m≠-1,
即m≥1或m<-1时,取等号,
由不等式f(x)≥$\frac{|3m+1|-|1-m|}{|m+1|}$对任意实数m≠=-1恒成立,得|x+1|-|x-3|≥2,
由(Ⅰ)中图象,可知x≥2,
所以实数x的取值范围是{x|x≥2}
点评 本题考查绝对值不等式的解法,同时考查不等式恒成立问题的求法,运用分类讨论的思想方法和绝对值不等式的性质是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
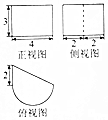
| A. | 14+6$\sqrt{5}$+10π | B. | 14+6$\sqrt{5}$+20π | C. | 12+12π | D. | 26+6$\sqrt{5}$+10π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18种 | B. | 24种 | C. | 48种 | D. | 36种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题,“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0“ | |
| B. | 对于命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn“是“em<en”的必要不充分条件 | |
| D. | 若p∨q为假命题,则p,q均为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
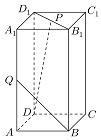 如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;
如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com