练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数y=f（x），下列说法错误的是（　　）
    A、△y=f（x0+△x）-f（x0）叫函数增量
    B、
    △y
    △x
    =
    f(x0+△x)-f(x0)
    △x
    叫函数在[x0，x0+△x]上的平均变化率
    C、f（x）在点x0处的导数记为y′
    D、f（x）在点x0处的导数记为f′（x0）
    考点：导数的运算
    专题：导数的概念及应用
    分析：根据导数的定义判断即可．
    解答： 解：根据导数的定义f′（x0）=
    lim
    △x→0
    f(x0+△x)-f(x0)
    △x
    ，
    即可判断出A，B，D正确，C错误，
    故选：C
    点评：本题考查导数的概念，考查学生分析解决问题的能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    实数的乘法运算与向量的数量积运算类比，不成立的运算律是（　　）
    A、a×b=b×a类比
    a
    •
    b
    =
    b
    •
    a
    B、a×（b×c）=（a×b）×c类比
    a
    •（
    b
    •
    c
    ）=（
    a
    •
    b
    ）•
    c
    C、a2=|a|2类比
    a
    •
    a
    =（
    a
    ）2=|
    a
    |2
    D、a（b+c）=ab+ac类比
    a
    •（
    b
    +
    c
    ）=
    a
    •
    b
    +
    a
    •
    c

    查看答案和解析>>

    科目：高中数学 来源： 题型：

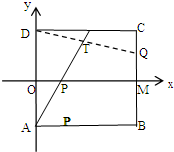    如图，矩形ABCD中，A（0，-1）D（0，1）B（2，-1）C（2，1），动点P在线段OM上运动，动点Q在线段CB上运动，保持|OP|=|CQ|，则直线AP与DQ的交点T的轨迹方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    程序框图是算法思想的重要表现形式，程序框图中不含（　　）
    A、流程线B、判断框
    C、循环框D、执行框

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如下：
    您是否需要志愿者男女
    需要4030
    不需要160270
    （Ⅰ）估计该地区老年人中，需要志愿提供帮助的老年人的比例；
    （Ⅱ）通过计算说明，你能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？
    附：
    P(K2≥k)
    k
     
    0.050
    3.841
     
    0.010
    6.625
      
    0.001
    10.828
        K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    y′=
    1
    x2
    ，则y可以是下列各式中的（　　）
    A、
    1
    x
    B、-
    x+1
    x
    C、-2x-3
    D、-
    1
    2x3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出以下命题：
    ①i是虚数单位，复数
    2i
    1+i
    的实部为1；
    ②命题p：“?x∈R+，sinx+
    1
    sinx
    ≥2”是真命题；
    ③已知线性回归方程为
    ?
    y
    =3+2x，当变量x增加2个单位，其预报值平均增加4个单位；
    ④把函数y=3sin（2x+
    π
    3
    ）的图象按向量
    n
    =（
    π
    3
    ，1）平移后得到y=1+3sin2x的图象；
    ⑤已知
    2
    2-4
    +
    6
    6-4
    =2，
    5
    5-4
    +
    3
    3-4
    =2，
    7
    7-4
    +
    1
    1-4
    =2，
    10
    10-4
    +
    -2
    -2-4
    =2，依照以上各式的规律，得到一般性的等式为
    n
    n-4
    +
    8-n
    (8-n)-4
    =2，（n≠4）．
    则正确命题的序号为
     
    （写出所有正确命题的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    将y=f′（x）sinx图象向左平移
    π
    4
    个单位，得y=1-2sin2x图象，则f（x）=（　　）
    A、2cosxB、2sinx
    C、sinxD、cosx

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某几何体的三视图如图所示，则该几何体的体积为
     
    ．

    查看答案和解析>>

    同步练习册答案