
科目: 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,AB=1,PA•AC=1,∠ABC=θ(0°<θ≤90°).
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,AB=1,PA•AC=1,∠ABC=θ(0°<θ≤90°).查看答案和解析>>
科目: 来源: 题型:解答题
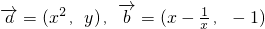 ,且
,且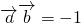 .如果存在正项数列{an}满足:
.如果存在正项数列{an}满足: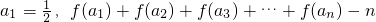 =a13+a23+a33+…+an3-n2an(n∈N*).
=a13+a23+a33+…+an3-n2an(n∈N*).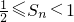 .
.查看答案和解析>>
科目: 来源: 题型:解答题
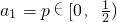 ,且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;
,且an+1=-2an2+2an,试判断{an}是否为周期数列,且说明理由;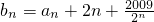 ,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.
,问是否存在最小的自然数n(n∈N*),使得对一切自然数m≥n,都有bm>2009?请说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:单选题
 +2013(a6-1)=1,
+2013(a6-1)=1, 则下列结论中正确的是
则下列结论中正确的是查看答案和解析>>
科目: 来源: 题型:解答题
 .
. 的值.
的值.查看答案和解析>>
科目: 来源: 题型:解答题
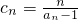 ,是否存在正整数p,q(1<p<q),使得c1,cp,cq成等比数列?若存在,求出所有的p,q的值;若不存在,请说明理由.
,是否存在正整数p,q(1<p<q),使得c1,cp,cq成等比数列?若存在,求出所有的p,q的值;若不存在,请说明理由.查看答案和解析>>
科目: 来源: 题型:解答题
 <t<2时,比较2n+2-n与tn+t-n的大小;
<t<2时,比较2n+2-n与tn+t-n的大小; <t<2,bn=
<t<2,bn=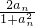 ,求证:
,求证: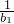 +
+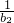 +…+
+…+ <2n-
<2n- .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com