
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
甲、乙两人轮流投一枚均匀硬币,甲先投,谁先得到正面则谁获胜.求:
(1)投币不超过4次即决定胜负的概率;
(2)在第4次时决定胜负的概率;
(3)甲获胜的概率;
(4)乙获胜的概率.
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
猎人在距离100m处射击一野兔,其命中率为 ,如果第一次射击未命中,则猎人进行第二次射击,但距离为150m;如果又未中,则猎人进行第三次射击,并且在发射瞬间距离为200m,此猎人命中概率与距离的平方成反比,求命中野兔的概率.
,如果第一次射击未命中,则猎人进行第二次射击,但距离为150m;如果又未中,则猎人进行第三次射击,并且在发射瞬间距离为200m,此猎人命中概率与距离的平方成反比,求命中野兔的概率.
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
计划用2000元购买单价为50元的桌子和20元的椅子,希望使桌椅的总数尽可能的多,但椅子数不少于桌子数,且不多于桌子数的1.5倍,桌、椅各买多少才行?
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
某厂使用A、B两种零件装配两种产品X、Y,该厂的生产能力是月产X最多2500件,月产Y最多1200件,而组装一件X需要4个A、2个B,组装一件Y需要6个A、8个B.某个月,该厂能用的A最多有14000个,B最多有12000个,已知产品X每件利润1000元,Y每件利润2000元,欲使该月利润最高,需组装X、Y产品各多少件?最高利润为多少万元?
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
平面上有两个向量 =(1,0),
=(1,0), =(0,1),今有动点P从P0(-1,2)开始沿着与向量|
=(0,1),今有动点P从P0(-1,2)开始沿着与向量| +
+ |相同的方向做匀速直线运动,速度大小为|
|相同的方向做匀速直线运动,速度大小为| +
+ |;另一动点Q从点Q0(-2,-1)出发,沿着与向量3
|;另一动点Q从点Q0(-2,-1)出发,沿着与向量3 +2
+2 相同的方向做匀速直线运动,速度大小为|3
相同的方向做匀速直线运动,速度大小为|3 +2
+2 |.设P、Q在时刻t=0s时分别在P0、Q0处,则当
|.设P、Q在时刻t=0s时分别在P0、Q0处,则当 ⊥
⊥ 时,用了多长时间?
时,用了多长时间?
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
设x、y∈R,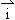 ,
, 为直角坐标平面内x,y轴正方向上的单位向量,若向量
为直角坐标平面内x,y轴正方向上的单位向量,若向量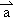 =x
=x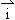 +(y+2)
+(y+2) ,
,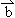 =x
=x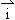 +(y-2)
+(y-2) ,且|
,且|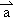 |+|
|+|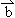 |=8.
|=8.
(1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点,设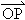 =
=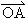 +
+ ,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使得四边形OAPB是矩形?若存在,求出直线l的方程;若不存在,试说明理由.
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
设 =(1+cosα,sinα),
=(1+cosα,sinα), =(1-cosβ,sinβ),
=(1-cosβ,sinβ), =(1,0),α∈(0,π),β∈(π,2π),
=(1,0),α∈(0,π),β∈(π,2π), 与
与 的夹角为θ1,
的夹角为θ1, 与
与 的夹角为θ2,且θ1-θ2=
的夹角为θ2,且θ1-θ2= ,求sin
,求sin 的值.
的值.
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
平面直角坐标系有点P(1,cosx),Q(cosx,1),(x∈[- ,
, ]).
]).
(1)求向量 和
和 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);
(2)求θ的最值.
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
已知平面上三个向量 ,
, ,
, 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为 .
.
(1)求证:( -
- )⊥
)⊥ ;
;
(2)若|k +
+ +
+ |>1,(k∈R),求k的取值范围.
|>1,(k∈R),求k的取值范围.
查看答案和解析>>
科目: 来源:黄冈重点作业·高三数学(下) 题型:044
已知 =(2,1),
=(2,1), =(1,7),
=(1,7), =(5,1),设X是直线OP上的一点(其中O为坐标原点).
=(5,1),设X是直线OP上的一点(其中O为坐标原点).
(1)求使 ·
· 取最小值时的
取最小值时的 .
.
(2)对(1)中求出的点X,求∠AXB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com