某公司计划2009年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司带来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？

函数f(x)是定义在(－2，2)上的奇函数，且在(－2，2)上单调递减，若f(m－1)＋f(2m－3)＞0，求m的取值范围．

已知集合，集合，集合．

(1)求A∩B；

(2)若A∪C＝A，求实数m的取值范围．

已知公差大于零的等差数列{a_n}的前n项和为S_n，且满足a₃a₄＝117，a₂＋a₅＝22．

(1)求通项a_n；

(2)若bn＝，数列{b_n}是等差数列，求非零常数c；

(3)求f(n)＝(n∈N^*)的最大值．

已知圆：C：x²＋(y－1)²＝5，直线L：mx－y＋1－m＝0

(1)求证：对m∈R，直线L与圆C总有两个交点；

(2)设直线L与圆C交于点A、B，若|AB|＝，求直线L的倾斜角；

(3)设直线L与圆C交于A、B，若定点P(1，1)满足＝，求此时直线L的方程．

设有关于x的一元二次方程x²＋2ax＋b²＝0．

(1)若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率；

(2)若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．

某校从参加高二年级期中考试的学生中抽出60名学生，将其数学成绩(均为整数)分成六段[40，50)，[50，60)…[90，100]后画出如下频率分布直方图．观察图形的信息，回答下列问题：

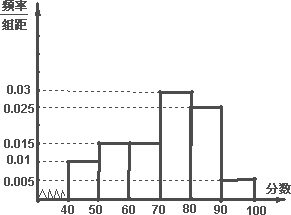
(1)估计这次考试的众数m与中位数n(结果保留一位小数)；

(2)估计这次考试的及格率(60分及以上为及格)和平均分．

已知等差数列{a_n}满足：a₃＝7，a₅＋a₇＝26，{a_n}的前n项和为S_n．

(Ⅰ)求a_n及S_n；

(Ⅱ)令b_n＝(n∈N^*)，求数列{b_n}的前n项和T_n．

第四届中国国际航空航天博览会于2010年11月在珠海举行，一架直升飞机在海拔800 m的高度飞行，一次飞行表演中从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如图所示)．试计算这个海岛的宽度PQ．

某中学生物兴趣小组在学校生物园地种植了一批名贵树苗，为了解树苗的生长情况，从这批树苗中随机地测量了其中50棵树苗的高度(单位：厘米)，并把这些高度列成了如下的频数分布表：

(1)在这批树苗中，其高度在85厘米以上的树苗大约有多少棵？

(2)这批树苗的平均高度大约是多少？；

(3)为了进一步获得研究资料，若从[40，50)组中移出一棵树苗，从[90，100)组中移出两棵树苗进行试验研究，则[40，50)组中的树苗A和[90，100)组中的树苗C同时被移出的概率是多少？