甲、乙两人进行围棋比赛，每盘比赛甲胜的概率为，乙胜的概率为，规定：某人胜3盘，则比赛结束．

(1)4盘结束比赛且甲获胜的概率是多少？

(2)比赛盘数的期望(精确到0.1)？

如图，四棱锥P－ABCD中，PB⊥底面ABCD，CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB＝AD＝PB＝3，BC＝6，点E在棱PA上且PE＝2EA．

(1)求异面直线PA与CD所成角；

(2)求证PC∥平面EBD；

(3)求二面角A－BE－D的大小．

已知向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，|a－b|＝．

(1)求cos(α－β)的值；

(2)若，且sinβ＝－，求sinα的值．

如图，已知三角形PAQ顶点P(－3，0)，点A在y轴上，点Q在x轴正半轴上，·＝0，＝2．

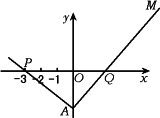
(1)当点A在y轴上移动时，求动点M的轨迹E的方程；

(2)设直线l：y＝k(x＋1)与轨迹E交于B、C两点，点D(1，0)，若∠BDC为钝角，求k的取值范围．

已知函数f(x)＝2n在[0，＋∞)上最小值是a_n(n∈N*)．

(1)求数列{a_n}的通项公式；

(2)已知数列{b_n}中，对任意n∈N*都有b_na＝1成立，设S_n为数列{b_n}的前n项和，证明：2S_n＜1；

(3)在点列A_n(2n，a_n)中是否存在两点A_i，A_j(i，j∈N*)，使直线A_iA_j的斜率为1？若存在，求出所有的数对(i，j)；若不存在，请说明理由．

已知函数f(x)的定义域为R，对任意的x₁，x₂都满足f(x₁＋x₂)＝f(x₁)＋f(x₂)，当x＞0时，f(x)＞0．

(1)试判断f(x)的奇偶性．

(2)试判断f(x)的单调性，并证明．

(3)若f(cos2θ－3)＋f(4m－2mcosθ)＞0对所有的θ∈[0，]恒成立，求实数m的取值范围．

如图，已知直平行六面体ABCD－A₁B₁C₁D₁中，AD⊥BD，AD＝BD＝a，E是CC₁的中点，AD⊥BE．

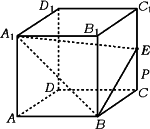
(1)求证：A₁D⊥平面BDE；

(2)求二面角B－DE－C的大小；

(3)求点B到平面A₁DE的距离．

口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标有数字3，第一次从口袋里任意抽取一张，放回口袋后第二次再任意抽取一张，记第一次与第二次取到卡片上数字之和为ξ．

(1)ξ为何值时，其发生的概率最大？说明理由．

(2)求随机变量ξ的期望Eξ．

已知向量a＝(1，1)，b＝(1，0)，c满足a·c＝0且|a|＝|c|，b·c＞0．

(1)求向量c；

(2)若映射f：(x，y)→(x₁，y₁)＝xa＋yc，求映射f下(1，2)的原象．

设x₁、x₂(x₁≠x₂)是函数f(x)＝ax³＋bx－a²x(a＞0)的两个极值点．

(1)若x₁＝－1，x₂＝2，求函数f(x)的解析式；

(2)若，求b的最大值．

(3)若x₁＜x＜x₂，且x₂＝a，函数，

求证：．