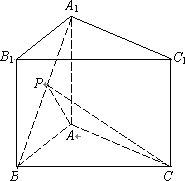
(理)在直三棱柱ABC－A₁B₁C₁中，底面△ABC是等腰直角三角形，∠BAC＝90°，P为A₁B的中点，且CP⊥A₁B，求二面角P―AC―B的大小．

已知数列｛a_n｝，a₁＝1，(n∈N^*)，数列｛b_n｝前n项之和，(n∈N^*)．

(1)求证成等差数列；

(2)求｛a_n｝，｛b_n｝通项公式；

(3)设，请你构造数列｛b_m｝，(m∈N*)使它前m项之和T_m≥c_n对任意n∈N^*恒成立，且恰好存在一个k₀∈N^*，使．

在△ABC中，已知A(0，a)，B(0，－a)，(a为不等于零的常数)AC、BC两边所在的直线分别与x轴交于原点同侧的点M、N．设C(x₀，y₀)．

(1)求M、N两点坐标(用(x₀，y₀)及α表示)．

(2)若M、N满足，求点C的轨迹方程；

(3)如果存在直线l∶y＝kx－1(k≠0)，使l与点C的轨迹相交于不同的P、Q两点，且，求α的取值范围．

为了研究“两个定义在R上的单调增函数f(x)，g(x)经过运算以后的单调性”这一问题，

(1)取f(x)＝2x＋1(x∈R)，g(x)＝3x－2(x∈R)，计算f(x)＋g(x)，f(x)－g(x)，判断其单调性，并将结论用数学语言表述；

(2)由(1)得出的关于单调性的结论，对R上的单调增函数f(x)，g(x)都成立吗？若成立，给出证明；若不成立，举出反例．

设复数z＝－3cosθ＋2isinθ．

(1)当时，求的值；

(2)若复数z所对应的点在直线x＋3：y＝0上，求的值．

已知动点M到定点(1，0)的距离比M到定直线x＝－2的距离小1．

(1)求证：M点轨迹为抛物线，并求出其轨迹方程；

(2)大家知道，过圆上任意一点P，任意作相互垂直的弦PA，PB，则弦AB必过圆心(定点)，受此启发，研究下面的问题：

①过(1)中的抛物线的顶点O任作相互垂直的弦OA，OB，则弦AB是否经过一个定点？若经过定点(设为Q)，请求出Q点的坐标，否则说明理由；

②研究：对于抛物线y²＝2px上顶点以外的定点是否也有这样的性质？请提出一个一般的结论，并证明．

直线x＋y＝n(n∈N^*)与x轴、y轴所围成区域内部(不包括边界)的整点个数为a_n，所围成区域内部(包括边界)的整点个数为b_n.(整点就是横坐标，纵坐标都为整数的点)

(1)求a₃和b₃的值；

(2)求a_n及b_n的表达式；

(3)对a_n个整点中的每一个点用红、黄、蓝、白四色之一着色，其方法总数为A_n，对b_n个整点中的每一个点用红、黄两色之一着色，其方法总数为B_n，试比较A_n与B_n的大小．

为了研究“两个定义在R上的单调增函数f(x)，g(x)经过运算以后的单调性”这一问题，

(1)、取f(x)＝2x＋1(x∈R)，g(x)＝3x－2(x∈R)，计算f(x)＋g(x)，f(x)－g(x)，判断其单调性，并将结论用数学语言表述．

(2)、由(1)得出的关于单调性的结论，对R上的单调增函数f(x)，g(x)都成立吗？若成立，给出证明；若不成立，举出反例；

(3)、请运用上述研究方法继续研究R上的单调增函数f(x)，g(x)经过其它某一种运算后的单调性．(只需要得出一个正确结论)

已知正四棱柱ABCD－A₁B₁C₁D₁中，底面边长AB＝2，侧棱BB₁＝4，过点B作B₁C的垂线交侧棱CC₁于点E，交B₁C于点F.

(1)求异面直线A₁B与B₁C所成角的大小；

(2)求证：A₁C⊥平面BED．

设复数z＝－3cosθ＋2isinθ

(1)当时，求的值；

(2)若复数z所对应的点在直线x＋3y＝0上，求的值．