已知函数f(x)与函数的图像关于直线y＝x对称．

(1)试用含a的代数式表示函数f(x)的解析式，并指出它的定义域；

(2)数列｛a_n｝中，a₁＝1，当n≥2时，a_n＞a₁．数列｛b_n｝中，b₁＝2，S_n＝b₁＋b₂＋…b_n．点在函数f(x)的图像上，求_a的值；

(3)在(2)的条件下，过点P_n作倾斜角为的直线l_n，则l_n在ｙ轴上的截距为，求数列｛a_n｝的通项公式．

已知a为实数，函数f(x)＝(x²＋)(x＋a)

(1)若函数f(x)的图象上有与x轴平行的切线，求a的取值范围；

(2)若(－1)＝0，(Ⅰ)求函数f(x)的单调区间；(Ⅱ)若对任意的x₁，x₂∈[－1，0]，不等式|f(x₁)－f(x₂)|≤m恒成立，试求m的最小值．

在平面直角坐标系中，已知A₁(－3，0)，A₂(3，0)，P(x，y)，M(，0)，若实数λ使向量，λ，满足λ²·()²＝·．

(1)求点P的轨迹方程，并判断P点的轨迹是怎样的曲线；

(2)当λ＝时，过点A₁且斜率为1的直线与此时(1)中的曲线相交的另一点为B，能否在直线x＝－9上找一点C，使ΔA₁BC为正三角形(请说明理由)．

如图①在直角梯形ABCP中，BC∥AP，AB⊥BC，CD⊥AP，AD＝DC＝PD＝2，E，F，G分别是线段PC、PD，BC的中点，现将ΔPDC折起，使平面PDC⊥平面ABCD(如图②)

(1)求证AP∥平面EFG；

(2)求二面角G－EF－D的大小；

(3)在线段PB上确定一点Q，使PC⊥平面ADQ，试给出证明．

四个纪念币A、B、C、D，投掷时正面向上的概率如下表所示(0＜a＜1)

这四个纪念币同时投掷一次，设ξ表示出正面向上的个数．

(1)求概率p(ξ)

(2)求在概率p(ξ)，p(ξ＝2)为最大时，a的取值范围．

已知函数f(x)＝＋2sin2x

(1)求函数f(x)的最大值及此时x的值；

(2)求函数f(x)的单调递减区间．

设f(x)＝(a＞0)为奇函数，且_min＝，数列{a_n}与{b_n}满足如下关系：a₁＝2，，．

(1)求f(x)的解析表达式；(2)证明：当n∈N₊时，有b_n．

已知椭圆为常数，且α＞1)，向量m＝(1，t)(t＞0)，过点A(－α，0)且以m为方向向量的直线与椭圆交于点B，直线BO交椭圆于点C(O为坐标原点)．

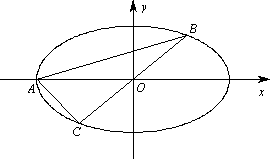
(Ⅰ)用t表示△ABC的面积S(t)；

(Ⅱ)若，求S(t)的最大值．

如图，在四棱锥P－ABCD中，底面ABCD是一直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝1，AD＝2，且PA⊥平面ABCD，PD与底面成30°角．

(Ⅰ)求证：平面APB⊥平面CPB；

(Ⅱ)求二面角A－PC－B的大小；

(Ⅲ)若AE⊥PD，E为垂足，求异面直线AE与CD所成角的大小．

口袋里装有红色和白色共36个不同的球，且红色球多于白色球．从袋子中取出2个球，若是同色的概率为，求：

(1)袋中红色、白色球各是多少？

(2)从袋中任取3个小球，至少有一个红色球的概率为多少？