在△ABC中，角A、B、C的对边分别为a、b、c，且满足(2a－c)cosB＝bcosC．

(Ⅰ)求角B的大小；

(Ⅱ)设的最大值是5，求k的值．

设函数f(x)＝(1＋x)²－ln(1＋x)²

(1)求函数f(x)的单调区间；

(2)当时，不等式f(x)＜m恒成立，求实数m的取值范围；

(3)关于x的方程f(x)＝x²＋x＋a在［0，2］上恰有两个相异实根，求a的取值范围．

已知，f(x)的反函数为g(x)，点在曲线y＝g(x)上(n∈N^*)，且a₁＝1

(I)求y＝g(x)的表达式；(II)证明数列{}为等差数列；

(Ⅲ)设，记S_n＝b₁＋b₂＋…＋b_n，求S_n

已知点A(4，0)，B(1，0)，动点P满足

(Ⅰ)求点P的轨迹C的方程；

(Ⅱ)点Q是轨迹C上一点，过点Q的直线l交x轴于点F(－1，0)，交y轴于点M，若．

美国蓝球职业联赛(NBA)某赛季的总决赛在湖人队与活塞队之间进行，比赛采取七局四胜制，即若有一队胜四场，则此队获胜且比赛结束．因两队实力非常接近，在每场比赛中每队获胜是等可能的．据资料统计，每场比赛组织者可获门票收入100万美元．求在这次总决赛过程中，(1)比赛5局湖人队取胜的概率；(2)比赛组织者获得门票收入ξ(万美元)的概率分布列及数学期望Eξ．

如下图，ABCD－A₁B₁C₁D₁是正四棱柱，侧棱长为3，底面边长为2，E是棱BC的中点．

(I)求证：BD₁∥平面C₁DE；

(II)求二面角C₁－DE－C的大小；

(III)在侧棱BB₁上是否存在点P，使得CP⊥平面C₁DE？证明你的结论

已知函数

(I)求f(x)的定义域；(II)设α的锐角，且f(a)的值．

已知四棱锥P-ABCD的底面是边长为a的菱形，∠ABC＝120°，又PC⊥平面ABCD，PC＝a，E是PA的中点．

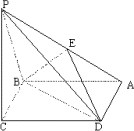
1)求证：平面EBD⊥平面ABCD；

2)求直线PB与直线DE所成的角的余弦值；

3)设二面角A－BE－D的平面角q ，求cosq 的值

设函数f(x)＝2cosx(cosx＋sinx)－1，xÎ R

(1)求f(x)最小正周期T；

(2)求f(x)单调递增区间；

(3)设点P₁(x₁，y₁)，P₂(x₂，y₂)，…，P_n(x_n，y_n)(nÎ N*)在函数f(x)的图象上，且满足条件：x₁＝，x_n＋₁－x_n＝，求N_n＝y₁＋y₂＋…＋y_n的值．

(1)请写出一个各项均为实数且公比0＜q＜1的等比数列，使得其同时满足a₁＋a₆＝11且；

(2)在符合(1)条件的数列中，能否找到一正偶数m，使得这三个数依次成等差数列?若能，求出这个m的值；若不能，请说明理由．