我们用min｛S₁，S₂，…，S_n｝和max｛S₁，S₂，…，S_n｝分别表示实数S₁，S₂，…，S_n中的最小者和最大者．

(1)设f(x)＝min｛sinx，cosx｝，g(x)＝max｛sinx，cosx｝，x∈［0，2π］，函数f(x)的值域为A，函数g(x)的值域为B，求A∩B；

(2)数学课上老师提出了下面的问题：设a₁，a₂，a_n为实数，x∈R，求函数(x₁＜x₂＜x_n∈R＝的最小值或最大值．为了方便探究，遵循从特殊到一般的原则，老师让学生先解决两个特例：求函数和的最值．学生甲得出的结论是：［f(x)］_min＝min｛f(－2)，f(－1)，f(1)｝，且f(x)无最大值．学生乙得出的结论是：［g(x)］_max＝max｛g(－1)，g(1)，g(2)｝，且g(x)无最小值．请选择两个学生得出的结论中的一个，说明其成立的理由；

(3)试对老师提出的问题进行研究，写出你所得到的结论并加以证明(如果结论是分类的，请选择一种情况加以证明)．

设三次函数在x＝1处取得极值，其图象在x＝m处的切线的斜率为－3a．

(1)求证：；

(2)若函数y＝f(x)在区间[s，t]上单调递增，求的取值范围；

(3)问是否存在实数k(k是与a，b，c，d无关的常数)，当x≥k时，恒有恒成立？若存在，试求出k的最小值；若不存在，请说明理由．

已知函数

(1)若b＝2且h(x)＝f(x)－g(x)存在单调递减区间，求a的取值范围；

(2)设函数f(x)的图象C₁与函数g(x)的图象C₂交于点P、Q，过线段PQ的中点R作x轴的垂线分别交C₁、C₂于点M、N，是否存在点R，使C₁在点M处的切线与C₂在点N处的切线平行？如果存在，请求出R的横坐标，如果不存在，请说明理由．

已知曲线C：xy＝1，过C上一点A_n(x_n，y_n)作一斜率的直线交曲线C于另一点A_n+1(x_n+1，y_n+1)，点列{A_n}的横坐标构成数列{x_n}其中

(1)求x_n与x_n+1的关系式．

(2)求证：数列是等比数列；

(3)求证：

某人口袋中有人民币50元3张，20元3张和10元4张．

(1)现从中任意取出若干张，求总数恰好等于80元的不同取法种数(用数字作答)；

(2)现从中任意取出3张，求总数超过80元的概率．

已知直线l：y＝kx＋k＋1，抛物线C：y²＝4x，和定点M(1，1)．

(1)当直线经过抛物线焦点F时，求点M关于直线l的对称点N的坐标，并判断点N是否在抛物线C上

(2)当k变化(k≠0)且直线l与抛物线C有公共点时，设点P(a，1)关于直线l的对称点为Q(x₀，y₀)，求x₀关于k的函数关系式x₀＝f(k)．并求P与M重合时，x₀的取值范围

设不等式组所表示的平面区域为D_n，记D_n内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n∈N^*)．

(1)求f(1)，f(2)的值及f(n)的表达式；

(2)记，若对于一切正整数n，总有T_n≤m成立，求实数m的取值范围；

(3)设S_n为数列{b_n}的前n项和，其中b_n＝2^f(n)，问是否存在正整数n，t，使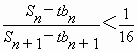成立？若存在，求出正整数n，t；若不存在，说明理由．

已知F₁(－2，0)，F₂(2，0)，点P满足，记点P的轨迹为E．

(1)求轨迹E的方程；

(2)若直线l过点F₂且与轨迹E交于P、Q两点．

(ⅰ)无论直线l绕点F₂怎样转动，在x轴上总存在定点M(m，0)，使MP⊥MQ恒成立，求实数m的值．

(ⅱ)过P、Q作直线的垂线PA、QB，垂足分别为A、B，记，求的取值范围．

已知f(x)＝x(x－a)(x－b)，点A(s，f(s))，B(t，f(t))

(I)若a＝b＝1，求函数f(x)的单调递增区间；

(II)若函数f(x)的导函数满足：当|x|≤1时，有||≤恒成立，求函数f(x)的解析表达式；

(III)若0＜a＜b，函数f(x)在x＝s和x＝t处取得极值，且，证明：与不可能垂直．