
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(文科) 题型:044
已知平面内任意一点P满足|PF1|+|PF2|=10,其中F1(0,-4)、F2(0,4)为平面内两个定点,
(1)求点P的轨迹方程.
(2)若O为原点,Q是OP的中点,M在F2Q上,且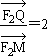 ,求点M的轨迹方程
,求点M的轨迹方程
查看答案和解析>>
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(文科) 题型:044
已知圆C圆心在x轴,且过两点A(-1,1),B![]()
(1)求圆C的方程
(2)设有点列Pn(n,0)(n∈N*),过点Pn(n=1,2……)引圆C的切线,若切线的斜率为kn,求和![]()
查看答案和解析>>
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(文科) 题型:044
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.

(Ⅰ)求证:AB1⊥平面A1BD;
(Ⅱ)求二面角A-A1D-B的大小.
查看答案和解析>>
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(文科) 题型:044
已知函数![]() .
.
(1)写出函数的单调递减区间;
(2)设![]() ,f(x)的最小值是-2,最大值是
,f(x)的最小值是-2,最大值是![]() ,求实数a、b的值.
,求实数a、b的值.
查看答案和解析>>
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(理科) 题型:044
设函数f(x)=3x2+1,g(x)=2x,现有数列{an}满足条件:对于n∈N*,an>0且f(an+1)-f(an)=g(an+1+![]() ),又设数列{bn}满足条件:bn=
),又设数列{bn}满足条件:bn=![]() (a>0且a≠1,n∈N*).
(a>0且a≠1,n∈N*).
(1)求证:数列{an}为等比数列;
(2)求证:数列![]() 是等差数列;
是等差数列;
(3)设k,L∈N**,且k+L=5,bk=![]() ,bL=
,bL=![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(4)如果k+L=M0(k,L∈N+,M0>3且M0是奇数),且bk=![]() ,bL=
,bL=![]() ,求从第几项开始an>1恒成立.
,求从第几项开始an>1恒成立.
查看答案和解析>>
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(理科) 题型:044
设函数![]() 的图象关于原点对称,f(x)的图象在点p(1,m)处的切线的斜率为-6,且当x=2时f(x)有极值.
的图象关于原点对称,f(x)的图象在点p(1,m)处的切线的斜率为-6,且当x=2时f(x)有极值.
(1)求a,b,c,d的值;
(2)若x1,x2∈[-1,1],求证:![]() .
.
查看答案和解析>>
科目: 来源:福建省福州八中2007-2008高三毕业班第三次质量检查数学试题(理科) 题型:044
已知A(3,0),B(0,3),C(cosα,sinα).
(1)若![]() 的值.
的值.
(2)O为坐标原点,若![]()
![]() .
.
查看答案和解析>>
科目: 来源:东莞市西夏中学2008届高三数学(理科)第一次高考模拟试卷 题型:044
已知a1=1,点(an,an+1)在函数f(x)=x2+4x+2的图象上,其中n=1,2,…
(1)证明:数列{lg(an+2)}是等比数列;
(2)设Tn=(a1+2)(a2+2)…(an+2),求Tn及数列{an}的通项公式;
(3)设![]() ,求数列{bn}的前n项和Sn,并证明
,求数列{bn}的前n项和Sn,并证明![]()
查看答案和解析>>
科目: 来源:东莞市西夏中学2008届高三数学(理科)第一次高考模拟试卷 题型:044
已知椭圆的两个焦点分别为F1(0,-2![]() ),F2(0,2
),F2(0,2![]() ),离心率
),离心率![]() .
.
(1)求椭圆方程;
(2)一条斜率为-9的直线l与椭圆交于不同的两点M、N,求线段MN中点横坐标x0的取值范围.
查看答案和解析>>
科目: 来源:东莞市西夏中学2008届高三数学(理科)第一次高考模拟试卷 题型:044
设函数![]() 是奇函数(a,b,c都是整数,且f(1)=2,f(2)<3.
是奇函数(a,b,c都是整数,且f(1)=2,f(2)<3.
(1)求a,b,c的值;
(2)当x<0,f(x)的单调性如何?用单调性定义证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com