取一切实数时，连接A(4sin，6cos)和B(－4cos，6sin)两点的线段的中点为M，求点M的轨迹．

已知函数f(x)＝ax²＋4x－2满足对任意x₁，x₂∈R且x₁≠x₂，都有．

(1)求实数a的取值范围；

(2)试讨论函数y＝f(x)在区间[－1，1]上的零点的个数；

(3)对于给定的实数a，有一个最小的负数M(a)，使得x∈[M(a)，0]时，－4≤f(x)≤4都成立，则当a为何值时，M(a)最小，并求出M(a)的最小值．

已知数列{a_n}、{b_n}、{c_n}的通项满足b_n＝a_n+1－a_n，c_n＝b_n+1－b_n(n∈N*)，若数列{b_n}是一个非零常数列，则称数列{a_n}是一阶等差数列；若数列{c_n}是一个非零常数列，则称数列{a_n}是二阶等差数列．

(Ⅰ)试写出满足条件a₁＝1、b₁＝1、c_n＝1的二阶等差数列{a_n}的前五项；

(Ⅱ)求满足条件(1)的二阶等差数列{a_n}的通项公式a_n；

(Ⅲ)若数列{a_n}首项a₁＝2，且满足c_n－b_n+1＋3a_n＝－2ⁿ⁺¹(n∈N*)，求数列{a_n}的通项公式a_n．

在△ABC中，a，b，c分别是角A，B，C的对边，已知，且．

求：(1)角B；

(2)a＋c的值．

已知α∈[0，π]，试讨论方程x²sinα＋y²cosα＝1所表示的曲线的类型．

已知曲线C是中心在原点，焦点在x轴上的双曲线的右支，它的右准线方程l：x＝，l与x轴交于E，一条渐近线方程是y＝x，线段PQ是过曲线C右焦点F的一条弦．

(1)求曲线C的方程；

(2)若R为PQ中点，且在直线l的左侧能作出直线m：x＝a，使点R在直线m上的射影S满足＝0，当P在曲线C上运动时，求a的取值范围；

(3)若过P作PM∥x轴交l于M，连MQ交x轴于H，求证H平分EF．

已知数列{a_n}及{b_n}其中a₁＝1，a_n＝2ⁿb_n，a_n+1－2a_n＝2ⁿ．

(1)求证{b_n}成等差数列；

(2)求数列{a_n}的通项公式；

(3)若函数f(x)＝－x²＋4x－对于一切正整数n都有f(x)≤0，求x的取值范围．

已知函数f(x)＝ax²＋bx＋c(≤a≤1)的图象过点A(0，1)且直线2x＋y－1＝0与y＝f(x)图象切于A点．

(1)求b与c的值；

(2)设f(x)在[1，3]上的最大值与最小值分别为M(a)、N(a)、g(x)＝M(a)－N(a)，若g(a)＝2，求实数a的值．

如图，直三棱柱ABC－A₁B₁C₁的底面ABC为等腰直角三角形，∠ACB＝90°，AC＝1，点C到AB₁的距离为CE＝，D为AB的中点．

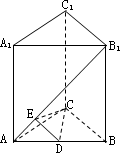
(1)求证：AB₁⊥平面CED；

(2)求异面直线AB₁与CD之间的距离；

(3)求二面角E－AC－D的大小．

已知动圆过定点P(1，0)，且与定直线L：x＝－1相切，点C在l上．

(1)求动圆圆心的轨迹M的方程；

(Ⅰ)问：△ABC能否为正三角形？若能，求点C的坐标；若不能，说明理由

(Ⅱ)当△ABC为钝角三角形时，求这种点C的纵坐标的取值范围．