
科目: 来源:浙江省金华一中2011-2012学年高一上学期期中考试数学试题(人教版) 题型:044
设函数f(x)=ax2+8x+3(a<0)
(1)a=-2时,对x∈[0,t](t>0),f(x)≥-5总成立,求t的最大值;
(2)对给定负数a,有一个最大正数g(a),使得在整个区间[0,g(a)]上,不等式|f(x)|≤5都成立,问:a为何值时,g(a)最大?
查看答案和解析>>
科目: 来源:安徽省师大附中2011-2012学年高一上学期期中考试数学试题(人教版) 题型:044
已知:函数f(x)对一切实数x,y都有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0.
(1)求f(0)的值.
(2)求f(x)的解析式.
(3)已知a∈R,设P:当0<x<![]() 时,不等式f(x)+3<2x+a恒成立;Q:当x∈[-2,2]时,g(x)=f(x)-ax是单调函数.如果满足P成立的a的集合记为A,满足Q成立的a的集合记为B,求A∩CRB(R为全集).
时,不等式f(x)+3<2x+a恒成立;Q:当x∈[-2,2]时,g(x)=f(x)-ax是单调函数.如果满足P成立的a的集合记为A,满足Q成立的a的集合记为B,求A∩CRB(R为全集).
查看答案和解析>>
科目: 来源:北京市101中学2011-2012学年高一上学期期中考试数学试题(人教版) 题型:044
设f(x)=3ax2-2bx+c,若a-b+c=0,f(0)>0,f(1)>0.
(1)求证:方程f(x)=0在区间(0,1)内有两个不等的实数根;
(2)若a,b,c都为正整数,求a+b+c的最小值.
查看答案和解析>>
科目: 来源:江苏省泰州中学2011-2012学年高一上学期期中考试数学试题(人教版) 题型:044
已知函数f(x)=ax+b,(a>0,a≠1).


(1)若f(x)的图像如图(1)所示,求a,b的值;
(2)若f(x)的图像如图(2)所示,求a,b的取值范围.
(3)在(1)中,若|f(x)|=m有且仅有一个实数解,求出m的范围.
查看答案和解析>>
科目: 来源:江苏省扬州市安宜高级中学2011-2012学年高二上学期期中考试数学试题(人教版) 题型:044
为了解某中学高二女生的身高情况,该校对高二女生的身高进行了一次随机抽样测量,所得数据整理后列出了频率分布表如下:(单位:cm)

(1)求出表中m、n、M、N所表示的数值;
(2)绘制频率分布直方图;

(3)估计该校女生身高小于162.5 cm的百分比.
查看答案和解析>>
科目: 来源:江苏省上冈高级中学2011-2012学年高二上学期期中考试数学理科试题 题型:044
已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤![]() (x+2)2成立.
(x+2)2成立.
(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
查看答案和解析>>
科目: 来源:江苏省徐州市丰县修远双语学校2011-2012学年高二上学期第二次月考数学试题 题型:044
(理科做)
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M是AB的中点.建立适当的空间直角坐标系,解决下列问题:
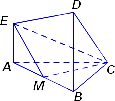
(1)求证:CM⊥EM;
(2)求CM与平面CDE所成角的大小.
查看答案和解析>>
科目: 来源:江苏省徐州市丰县修远双语学校2011-2012学年高二上学期第二次月考数学试题 题型:044
如图,在四棱锥P-ABCD中,四边形ABCD是正方形,PA⊥平面ABCD,PA=AB=2,且E,F分别是BC,CD的中点.

(1)求证:平面PEF⊥平面PAC;
(2)求三棱锥P-EFC的体积.
查看答案和解析>>
科目: 来源:福建省安溪一中、惠安一中、养正中学2011-2012学年高一上学期期中联考数学试题 题型:044
若函数f(x)满足下列条件:在定义域内存在x0,使得f(x0+1)=f(x0)+f(1)成立,则称函数f(x)具有性质M;反之,若x0不存在,则称函数f(x)不具有性质M.
(Ⅰ)证明:函数f(x)=2x具有性质M,并求出对应的x0的值;
(Ⅱ)已知函数h(x)=lg![]() 具有性质M,求a的取值范围;
具有性质M,求a的取值范围;
(Ⅲ)试探究形如①y=kx+b(k≠0)、②y=ax2+bx+c(a≠0)、③y=![]() (k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.
(k≠0)、④y=ax(a>0且a≠1)、⑤y=logax(a>0且a≠1)的函数,指出哪些函数一定具有性质M?并加以证明.
查看答案和解析>>
科目: 来源:河北省衡水中学2011-2012学年高二上学期期中考试数学理科试题 题型:044
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点B恰好是抛物线![]() 的焦点,离心率等于
的焦点,离心率等于![]() .直线l与椭圆C交于M,N两点.
.直线l与椭圆C交于M,N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)椭圆C的右焦点F是否可以为△BMN的垂心?若可以,求出直线l的方程;若不可以,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com