如图，考虑点A(1，0)，(cosα，sinα)，(cosβ，－sinβ)，P(cos(α＋β)，sin(α＋β))．你能从这个图出发，推导出公式cos(α＋β)＝cosαcosβ－sinαsinβ吗？

，

．

分析上述各式的共同特点，写出能反映一般规律的等式，并对等式的正确性作出证明．

平面直角坐标系内的向量都可以用一有序实数对唯一表示，这使我们想到可以用向量作为解析几何的研究工具．如图，设直线l的倾斜角为α(α≠90°)．在l上任取两个不同的点，，不妨设向量的方向是向上的，那么向量的坐标是()．过原点作向量，则点P的坐标是()，而且直线OP的倾斜角也是α．根据正切函数的定义得

这就是《数学2》中已经得到的斜率公式．上述推导过程比《数学2》中的推导简捷．你能用向量作为工具讨论一下直线的有关问题吗？例如：

(1)过点，平行于向量的直线方程；

(2)向量(A，B)与直线的关系；

(3)设直线和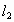的方程分别是

，

，

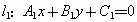
那么，∥，的条件各是什么？如果它们相交，如何得到它们的夹角公式？

(4)点到直线的距离公式如何推导？

在△ABC中，若，那么点O在△ABC的什么位置？

某人在静水中游泳，速度为千米/时．他在水流速度为4千米/时的河中游泳．

(1)如果他垂直游向河对岸，那么他实际沿什么方向前进？实际前进的速度为多少？

(2)他必须朝哪个方向游，才能沿与水流垂直的方向前进？实际前进的速度为多少？

已知对任意平面向量，把绕其起点沿逆时针方向旋转θ角得到向量，叫做把点B绕点A逆时针方向旋转θ角得到点P．

(1)已知平面内点A(1，2)，点B(，)．把点B绕点A沿顺时针方向旋转后得到点P，求点P的坐标；

(2)设平面内曲线C上的每一点绕坐标原点沿逆时针方向旋转后得到的点的轨迹是曲线，求原来曲线C的方程．

一条河的两岸平行，河的宽度d＝500m，一艘船从A处出发到河对岸．已知船的静水速度，水流速度．要使船行驶的时间最短，那么船行驶的距离与合速度的比值必须最小．此时我们分三种情况讨论：

(1)当船逆流行驶，与水流成钝角时；

(2)当船顺流行驶，与水流成锐角时；

(3)当船垂直于对岸行驶，与水流成直角时．

以初速度，抛射角θ投掷铅球，求铅球上升的最大高度和最大投掷距离．

△ABC中，D、E、F分别是AB、BC、CA的中点，BF与CD交于点O，设，，

(1)证明A、O、E三点在同一直线上，且；

(2)用a、b表示向量．

平面向量的数量积a·b是一个非常重要的概念，利用它可以容易地证明平面几何的许多命题，例如勾股定理、菱形的对角线相互垂直、长方形对角线相等、正方形的对角线垂直平分等．请你给出具体证明．