
科目: 来源:2008年普通高等学校招生全国统一考试 全国卷1(冀、豫、晋、桂)、数学(理) 题型:044
设函数f(x)=x-xlnx.数列{an}满足0<a1<1,an+1=f(an).
(Ⅰ)证明:函数f(x)在区间(0,1)是增函数;
(Ⅱ)证明:an<an+1<1;
(Ⅲ)设b∈(a1,1),整数![]() .证明:ak+1>b.
.证明:ak+1>b.
查看答案和解析>>
科目: 来源:2008年普通高等学校招生全国统一考试 全国卷1(冀、豫、晋、桂)、数学(理) 题型:044
已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性的即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(Ⅰ)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(Ⅱ)![]() 表示依方案乙所需化验次数,求
表示依方案乙所需化验次数,求![]() 的期望.
的期望.
查看答案和解析>>
科目: 来源:2008年普通高等学校招生全国统一考试 全国卷1(冀、豫、晋、桂)、数学(理) 题型:044
已知函数f(x)=x3+ax2+x+1,a∈R.
(Ⅰ)讨论函数f(x)的单调区间;
(Ⅱ)设函数f(x)在区间![]() 内是减函数,求a的取值范围.
内是减函数,求a的取值范围.
查看答案和解析>>
科目: 来源:2008年普通高等学校招生全国统一考试 全国卷1(冀、豫、晋、桂)、数学(理) 题型:044
设△ABC的内角A,B,C所对的边长分别为a,b,c,且![]() .
.
(Ⅰ)求tanAcotB的值;
(Ⅱ)求tan(A-B)的最大值.
查看答案和解析>>
科目: 来源:2008年天河区理科数学模拟卷(一) 题型:044
解答须写出文字说明、证明过程和演算步骤.
下图是一个直三棱柱(以A1B1C1为底面),被一平面所截得的几何体,截面为ABC.已知A1B1=B1C1=1,∠A1B1C1=90°,AA1=4,BB1=2,CC1=3
(Ⅰ)设点O是AB的中点,证明:OC∥平面A1B1C1
(Ⅱ)求AB与平面AA1CC1所成角的正弦值.
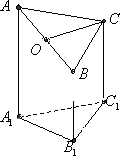
查看答案和解析>>
科目: 来源:2008年天河区理科数学模拟卷(一) 题型:044
解答须写出文字说明、证明过程和演算步骤.
已知角A,B,C为△ABC的三个内角,其对边分别为a,b,c,若![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)若△ABC的面积![]() ,求b+c的值.
,求b+c的值.
(Ⅱ)求取值范围.
查看答案和解析>>
科目: 来源:乌鲁木齐2008年高三年级第三次诊断性测验文理科数学试卷及详解答案 题型:044
(理科)已知焦点为F1(-1,0),F2(1,0)的椭圆经过点![]() ,直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
,直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
(Ⅰ)求![]() 的范围;
的范围;
(Ⅱ)若![]() 与向量
与向量![]() 共线,求
共线,求![]() 的值及△AOB的外接圆的方程.
的值及△AOB的外接圆的方程.
查看答案和解析>>
科目: 来源:乌鲁木齐2008年高三年级第三次诊断性测验文理科数学试卷及详解答案 题型:044
(文科)已知焦点为F1(-1,0),F2(1,0)的椭圆经过点![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设P是椭圆上的点,△PF1F2的外接圆为⊙C,求半径最小时⊙C的方程.
查看答案和解析>>
科目: 来源:乌鲁木齐2008年高三年级第三次诊断性测验文理科数学试卷及详解答案 题型:044
已知曲线f(x)=x2+2x在点(x1,f(x1))处的切线为l.
(Ⅰ)求l的方程;
(Ⅱ)设g(x)=(x+a)f(x),若g(x)在[1,2]上是增函数,求实数a的取值范围;
(Ⅲ)试判断l能否与曲线g(x)=ln(x+1)相切?并说明理由.
查看答案和解析>>
科目: 来源:乌鲁木齐2008年高三年级第三次诊断性测验文理科数学试卷及详解答案 题型:044
某选手在电视抢答赛中答对每道题的概率都是![]() ,答错每道题的概率都是
,答错每道题的概率都是![]() ,答对一题积1分,答错一题积-1分,答完n道题后的总积分记为Sn.
,答对一题积1分,答错一题积-1分,答完n道题后的总积分记为Sn.
(Ⅰ)答完2道题后,求同时满足S1=1且S2≥0的概率;
(Ⅱ)答完5道题后,求同时满足S1=1且S5=1的概率;
(Ⅲ)答完5道题后,设ξ=|S5|,求ξ的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com