水库的蓄水量随时间而变化，现用t表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量(单位：亿立方米)关于t的近似函数关系式为V(t)＝

(Ⅰ)该水库的蓄求量小于50的时期称为枯水期．以i－1＜t＜t表示第1月份(i＝1，2，…，12)，同一年内哪几个月份是枯水期？

(Ⅱ)求一年内该水库的最大蓄水量(取e＝2.7计算)．

已知函数f(t)＝．

(Ⅰ)将函数g(x)化简成Asin(ωx＋φ)＋B(A＞0，ω＞0，φ∈[0，2π])的形式；

(Ⅱ)求函数g(x)的值域．

设b＞0，椭圆方程为，抛物线方程为x²＝8(y－b)．如图所示，过点F(0，b＋2)作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点F₁．

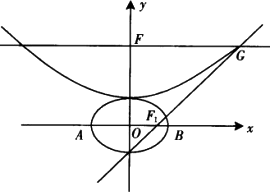
(1)求满足条件的椭圆方程和抛物线方程；

(2)设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得△ABP为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标)．

某初级中学共有学生2000名，各年级男、女生人数如下表：

已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19．

(1)求x的值；

(2)现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？

(3)已知y≥245，z≥245，求初三年级中女生比男生多的概率．

设p，q为实数，α，β是方程x²－px＋q＝0的两个实根，数列{x_n}满足x₁＝p，x₂＝p²－q，x_n＝px_n－1－qx_n－2(n＝3，4，…)．(1)证明：α＋β＝p，αβ＝q；(2)求数列{x_n}的通项公式；(3)若p＝1，，求{x_n}的前n项和S_n．

如图所示，四棱锥P－ABCD的底面ABCD是半径为R的圆的内接四边形，其中BD是圆的直径，∠ABD＝60°，∠BDC＝45°，PD垂直底面ABCD，，E，F分别是PB，CD上的点，且，过点E作BC的平行线交PC于G．

(1)求BD与平面ABP所成角θ的正弦值；

(2)证明：△EFG是直角三角形；

(3)当时，求△EFG的面积．

设k∈R，函数，F(x)＝f(x)－kx，x∈R，试讨论函数F(x)的单调性．

如图，椭圆(a＞b＞0)的一个焦点为F(1，0)，且过点(2，0)．

(Ⅰ)求椭圆C的方程；

(Ⅱ)若AB为垂直于x轴的动弦，直线l：x＝4与x轴交于点N，直线AF与BN交于点M．

(ⅰ)求证：点M恒在椭圆C上；

(ⅱ)求△AMN面积的最大值．

已知{a_n}是正数组成的数列，a₁＝1，且点()(n∈N*)在函数y＝x²＋1的图象上．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若列数{b_n}满足b₁＝1，b_n+1＝b_n＋2^an，求证：b_n·b_n+2＜b²_n+1．

三人独立破译同一份密码．已知三人各自破译出密码的概率分别为且他们是否破译出密码互不影响．

(Ⅰ)求恰有二人破译出密码的概率；

(Ⅱ)“密码被破译”与“密码未被破译”的概率哪个大？说明理由．