已知函数的最大值是1，其图像经过点．

(1)求f(x)的解析式；(2)已知，且求f(α－β)的值．

设b＞0，椭圆方程为，抛物线方程为x²＝8(y－b)．如图所示，过点F(0，b＋2)作x轴的平行线，与抛物线在第一象限的交点为G，已知抛物线在点G的切线经过椭圆的右焦点F₁．

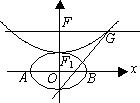
(1)求满足条件的椭圆方程和抛物线方程；

(2)设A，B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得△ABP为直角三角形？若存在，请指出共有几个这样的点？并说明理由(不必具体求出这些点的坐标)．

随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润(单位：万元)为．

(1)求的分布列；(2)求1件产品的平均利润(即的数学期望)；

(3)经技术革新后，仍有四个等级的产品，但次品率降为1％，一等品率提高为70％．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

已知函数，x∈R的最大值是1，其图像经过点．

(1)求f(x)的解析式；(2)已知，且，，求f(α－β)的值．

已知函数f(x)＝x³＋mx²＋nx－2的图象过点(－1，－6)，且函数的图象关于y轴对称．

(Ⅰ)求m、n的值及函数y＝f(x)的单调区间；

(Ⅱ)若a＞0，求函数y＝f(x)在区间(a－1，a＋1)内的极值．

如图，在四棱锥P－ABCD中，侧面PAD⊥底面ABCD，侧棱PA＝PD＝，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD＝2AB＝2BC＝2，O为AD中点．

(Ⅰ)求证：PO⊥平面ABCD；

(Ⅱ)求异面直线PB与CD所成角的余弦值；

(Ⅲ)求点A到平面PCD的距离．

已知函数f(x)＝ln(1＋x)－x₁

(Ⅰ)求f(x)的单调区间；

(Ⅱ)记f(x)在区间[0，π](n∈N*)上的最小值为b_x令a_n＝ln(1＋n)－b_x．

(Ⅲ)如果对一切n，不等式恒成立，求实数c的取值范围；

(Ⅳ)求证：

如图、椭圆的一个焦点是F(1，0)，O为坐标原点．

(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；

(Ⅱ)设过点F的直线l交椭圆于A、B两点．若直线l绕点F任意转动，值有|OA|²＋|OB|²|AB|²，求a的取值范围．

如图，在四棱锥P－ABCD中，则面PAD⊥底面ABCD，侧棱PA＝PD＝，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD＝2AB＝2BC＝2，O为AD中点．

(Ⅰ)求证：PO⊥平面ABCD；

(Ⅱ)求异面直线PD与CD所成角的大小；

(Ⅲ)线段AD上是否存在点Q，使得它到平面PCD的距离为？若存在，求出的值；若不存在，请说明理由．

已知向量m＝(sinA，cosA)，n＝，m·n＝1，且A为锐角．

(Ⅰ)求角A的大小；(Ⅱ)求函数f(x)＝cos2x＋4cosAsinx(x∈R)的值域．