在甲、乙两个盒子中分别装有标号为1，2，3，4的四个小球，现从甲、乙两个盒子中各取出一个小球，每个小球被取出的可能性相等．

(Ⅰ)求取出的两个小球上的标号为相邻整数的概率；

(Ⅱ)求取出的两个小球上的标号之间和能被3整除的概率；

(Ⅲ)球取出的两个小球上的标号只和大于5的概率

已知数列{a_a}中，a₁＝，点(n，2a_a+1－a_a)在直线y＝x上，其中n＝1，2，3…

(Ⅰ)令b_n＝a_n+1－a_n－1，求证数列{b_n}是等比数列；

(Ⅱ)球数列{a_a}的通项

已知＝(2，cosx)＝(sin(x＋)，－2)，函数f(x)·(x∈R)

(1)求函数f(x)的单调增区间；

(2)若f(x)＝，求cos(2x－)的值；

设函数f(x)＝x²－2(－1)^klnx(k∈N^*)，表示f(x)导函数．

(Ⅰ)求函数一份(x)的单调递增区间；

(Ⅱ)当k为偶数时，数列{a_n}满足a₁＝1，．证明：数列{a_n²}中不存在成等差数列的三项；

(Ⅲ)当k为奇数时，设，数列{b_n}的前n项和为S_n，证明不等式对一切正整数n均成立，并比较S₂₀₀₉－1与ln2009的大小．

已知双曲线x²－2y²＝2的左、右两个焦点为F₁，F₂，动点P满足|PF₁|＋|PF₂|＝4．

(Ⅰ)求动点P的轨迹E的方程；

(1I)设，过F₂且不垂直于坐标轴的动直线l交轨迹E于A、B两点，若DA、DB为邻边的平行四边形为菱形，求直线l的方程

定义在[－1，1]上的奇函数，已知当x∈[－1，0]时的解析式

(1)写出f(x)在[0，1]上的解析式；

(2)求f(x)在[0，1]上的最大值．

△ABC中，a，b，c分别是角A，B，C的对边，向量m＝(2sinB，2－cos2B)，，m⊥n，

(Ⅰ)求角B的大小；

(Ⅱ)若，b＝1，求c的值．

已知离心率为的椭圆的中心在远点，焦点在x轴上．双曲线以椭圆的长轴为实轴，短轴为虚轴，且焦距为

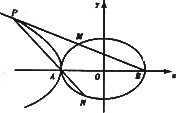
(I)求椭圆及双曲线的方程；

(2)设椭圆的左、右定点分别为A、B，在第二象限内取双曲线上一点P，连接BP交椭圆于点M，连接PA并延长交椭圆于点N，若求四边形ANBM的面积．

已知函数f(x)＝x³＋ax²＋bx．

(Ⅰ)若函数y＝f(x)在x＝2处有极值－6，求y＝f(x)的单调递减区间；

(Ⅱ)若y＝f(x)的导数对x∈[－1，1]都有求的范围．

班级联欢时，主持人拟出了如下一些节目：跳双人舞、独唱、朗诵等，指定3个男生和2个女生来参与，把5个人分别编号为1，2，3，4，5，其中1，2，3号是男生，4，5号是女生，将每个人的号分别写在5张相同的卡片上，并放入一个箱子中充分混合，每次从中随即地取出一张卡片，取出谁的编号谁就参与表演节目．

(Ⅰ)为了选出2人来表演双人舞，连续抽取2张卡片，求取出的2人不全是男生的概率；

(Ⅱ)为了选出2人分别表演独唱和朗诵，抽取并观察第一张卡片后，又放回箱子中，充分混合后再从中抽取第二张卡片，求：独唱和朗诵由同一个人表演的概率．