
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
已知点A,B分别是直线y=x和y=-x的动点(A,B在y轴的同侧),且△OAB的面积为![]() ,点P满足
,点P满足![]() .
.
(1)试求点P的轨迹C的方程;
(2)已知F![]() ,过O作直线l交轨迹C于两点M,N,若
,过O作直线l交轨迹C于两点M,N,若![]() ,试求△MFN的面积.
,试求△MFN的面积.
(3)理:已知F![]() ,矩形MFNE的两个顶点M,N均在曲线C上,试求矩形MFNE面积的最小值.
,矩形MFNE的两个顶点M,N均在曲线C上,试求矩形MFNE面积的最小值.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
已知动点P到直线![]() 的距离是到定点(
的距离是到定点(![]() )的距离的
)的距离的![]() 倍.
倍.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)如果直线l∶y=k(x+1)(k≠0)与P点的轨迹有两个交点A、B,求弦AB的垂直平分线在y轴上的截距y0的取值范围.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
小明一家三口都会下棋.在假期里的每一天,父母都交替与小明下三盘棋,已知
(1)小明胜父亲的概率是![]() ,胜母亲的概率是
,胜母亲的概率是![]() .如果小明与父亲先下,求小明恰胜一盘的概率;
.如果小明与父亲先下,求小明恰胜一盘的概率;
(2)父母与小明约定,只要他在三盘中能至少连胜两盘,就给他奖品,那么小明为了获胜希望更大,他应该先与父亲下,还是先与母亲下?请用计算说明理由.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
文:某自助银行共有4台ATM机,在某一时刻A、B、C、D四台ATM机被占用的概率分别为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(Ⅰ)如果某客户只能使用A或B型号的ATM机,求该客户需要等待的概率;
(Ⅱ)求至多有三台ATM机被占用的概率;
(Ⅲ)求恰有两台ATM机被占用的概率.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
理:某自助银行共有4台ATM机,在某一时刻A、B、C、D四台ATM机被占用的概率分别为![]() 、
、![]() 、
、![]() 、
、![]() ,设某一时刻这家自助银行被占用的ATM机的台数为ξ
,设某一时刻这家自助银行被占用的ATM机的台数为ξ
(Ⅰ)如果某客户只能使用A或B型号的ATM机,求该客户需要等待的概率;
(Ⅱ)求至多有三台ATM机被占用的概率;
(Ⅲ)求ξ的分布列和数学期望.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
如图,二面角P-CB-A为直二面角,∠PCB=90°,∠ACB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2,PM=1.
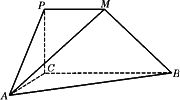
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的正切值;
(Ⅲ)求点P到平面ABM的距离.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
无穷数列{an}满足:![]() (λ≥0为常数).
(λ≥0为常数).
(1)若a1=1且数列{nan}为等比数列,求λ;
(2)已知a1=1,λ=3,若50<am<80,求m;
(3)若存在正整数N,使得当n>N时,有an+1<an,求证:存在正整数M,使得当n>M时,有an<0.
查看答案和解析>>
科目: 来源:北京市海淀区2009年高三数学查漏补缺题 题型:044
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.
(1)求C的大小;
(2)求sinA+sinB的最大值.
查看答案和解析>>
科目: 来源:东北育才学校2008-2009学年度高三模拟试题(理科数学) 2009.5.20 题型:044
已知函数f(x)=ex-ex.
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)求证:![]() (n∈N*);
(n∈N*);
(Ⅲ)对于函数h(x)与g(x)定义域上的任意实数x,若存在常数k,b,使得h(x)≥kx+b和g(x)≤kx+b都成立,则称直线y=kx+b为函数h(x)与g(x)的“分界线”设函数![]() ,g(x)=elnx,h(x)与g(x)是否存在“分界线”?若存在,求出k,b的值;若不存在,请说明理由.
,g(x)=elnx,h(x)与g(x)是否存在“分界线”?若存在,求出k,b的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:东北育才学校2008-2009学年度高三模拟试题(理科数学) 2009.5.20 题型:044
已知椭圆C的方程![]() ,直线l与椭圆C交于A,B两点,且OA⊥OB(O为坐标原点),OH⊥AB于H点.
,直线l与椭圆C交于A,B两点,且OA⊥OB(O为坐标原点),OH⊥AB于H点.
(Ⅰ)求点H的轨迹方程;
(Ⅱ)设M为(Ⅰ)中轨迹上的动点,点![]() ,求∠OMN的最大值.
,求∠OMN的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com