如图，在Rt△ABC中，∠BAC＝90°，A(－，1)、B(，1)，S_△ABC＝(平方单位)，动点P在曲线E(y≥1)上运动，若曲线E过点C且满足|PA|＋|PB|的值为常数．

(Ⅰ)求曲线E的方程；

(Ⅱ)设直线l的斜率为1，若直线l与曲线E有两个不同的交点P、Q，求线段PQ的中点M的轨迹方程．

(设点O是直角坐标系的原点，点M在直线l∶x＝－p(p＞0)上移动，动点在线段MO的延长线上，且满足|MN|＝|MO|·|NO|．

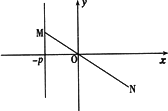
(Ⅰ)求动点N的轨迹方程；

(Ⅱ)当p＝1时，求|MN|的最小值．

如图，一载着重危病人的火车从O地出发，沿射线OA行驶，其中tanα＝在距离O地5a(a为正数)公里北偏东β角的N处住有一位医学专家，其中sinβ＝，现有110指挥部紧急征调离O地正东p公里的B处的救护车赶往N处载上医学专家全速追赶乘有重危病人的火车，并在C处相遇，经测算当两车行驶的路线与OB围成的三角形OBC面积S最小时，抢救最及时．

(1)求S关于p的函数关系；

(2)当p为何值时，抢救最及时．

已知＝(x，0)，＝(1，y)，(＋)⊥(－)

(1)求点P(x，y)的轨迹C的方程；

(2)若直线L∶y＝kx＋m(m≠0)与曲线C交于A、B两点，D(0，－1)，且有|AD|＝|BD|，试求m的取值范围．

已知直线l∶y＝x＋k经过椭圆C∶的右焦点F₂，且与椭圆C交于A、B两点，若以弦AB为直径的圆经过椭圆的左焦点F₁，试求椭圆C的方程．

如图，线段AB(AB不与x轴垂直)过x轴正半轴上一点M(m，0)(m＞0)端点A，B到x轴距离之积为2m，以x轴为对称轴，过A，O，B三点作抛物线．

(1)求抛物线方程；

(2)若tan∠AOB＝－1，求m的取值范围．

已知：如图，过椭圆c∶(a＞b＞1)的左焦点F(－c，0)作垂直于长轴A₁A₂的直线与椭圆c交于P、Q两点，l为左准线．

(Ⅰ)求证：直线PA₂、A₁Q、l共点；

(Ⅱ)若过椭圆c左焦点F(－c，0)的直线斜率为k，与椭圆c交于P、Q两点，直线PA₂、A₁Q、l是否共点，若共点请证明，若不共点请说明理由．

已知大西北的荒漠上的A、B两地相距2 km，现准备在荒漠上围成一片以AB为一条对角线的平行四边形区域建成农艺园．按照规划，围墙的总长为8 km．

(1)农艺园的最大面积能达到多少？

(2)又该荒漠上有一条水沟P恰好经过A，且水沟P与AB成30°角．现欲对整个水沟进行加固改造，但对水沟可能被农艺园围进的部分暂不加固．问水沟暂时不加固的部分有多长？

某地区原有森林木材存量为a，且每年的增长率为25％，因生产建设的需要，每年年底要砍伐的木材量为b，设a_n为n年后该地区的森林木材存量，

(1)求a_n的表达式；

(2)为保护生态环境，防止水土流失，该地区每年的森林木材存量应不少于，如果b＝，那么该地区今后会发生水土流失吗？若会，要经过几年？(取lg2＝0.30)

在交通拥挤地段，为了确保交通安全，规定机动车相互之间的距离d(米)与车速v(千米/小时)需遵循的关系是d≥(其中a(米)是车身长，a为常量)，同时规定d≥，

(1)当d＝时，求机动车车速的变化范围；

(2)设机动车每小时流量Q＝，应规定怎样的车速，才能使机动车每小时流量Q最大？