如图，在直三棱柱ABC－A₁B₁C₁中，AC＝3，BC＝4，AB＝5，AA₁＝4，点D是AB的中点．

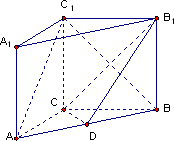
(Ⅰ)求证：AC⊥BC₁；

(Ⅱ)求证：AC₁∥平面CDB₁．

(Ⅲ)求CB₁与平面AA₁B₁B所成的角的正切值．

已知，，且0＜β＜α＜．

(Ⅰ)求tan2α的值；

(Ⅱ)求β．

已知函数在[1，＋∞)上为增函数，且∈(0，π)，，m∈R．

(1)求的值；

(2)若f(x)－g(x)在[1，＋∞)上为单调函数，求m的取值范围；

(3)设，若在[1，e]上至少存在一个x₀，使得f(x₀)－g(x₀)＞h(x₀)成立，求m的取值范围．

已知圆O：x²＋y²＝8交x轴于A，B两点，曲线C是以AB为长轴，直线：x＝－4为准线的椭圆．

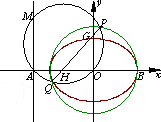
(1)求椭圆的标准方程；

(2)若M是直线上的任意一点，以OM为直径的圆K与圆O相交于P，Q两点，求证：直线PQ必过定点E，并求出点E的坐标；

(3)如图所示，若直线PQ与椭圆C交于G，H两点，且，试求此时弦PQ的长．

如图所示，等腰△ABC的底边AB＝，高CD＝3，点E是线段BD上异于点B，D的动点，点F在BC边上，且EF⊥AB，现沿EF将△BEF折起到△PEF的位置，使PE⊥AE，记BE＝x，V(x)表示四棱锥P－ACFE的体积．

(1)求V(x)的表达式；

(2)当x为何值时，V(x)取得最大值？

(3)当V(x)取得最大值时，在线段AC上取一点M，使得AM＝，求证：MF∥平面APE．

一个盒子装有六张卡片，上面分别写着如下六个定义域为R的函数：f₁(x)＝x，f₂(x)＝x²，f₃(x)＝x³，f₄(x)＝sinx，f₅(x)＝cosx，f₆(x)＝2．

(1)现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；

(2)现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ζ的分布列和数学期望．

已知A，B是△ABC的两个内角，(其中是互相垂直的单位向量)，若．

(1)试问tanA·tanB是否为定值，若是定值，请求出，否则说明理由；

(2)求tanC的最大值，并判断此时三角形的形状．

在数列{a_n}中，如果对任意n∈N*都有(k是不为零的常数)，则称{a_n}为等差比数列，k称为公差比．

(1)证明：公比不为1的等比数列是等差比数列，且公比等于公差比；

(2)判断两个数列a_n+1＝2a_n－1(a_n≠1)，b_n＝－λⁿ＋2是否为等差比数列；

(3)若数列{c_n}是首项为c₁＝a且c₂＝b(a≠b)，公差比为k的等差比数列，求{c_n}的通项公式．

如图，某地为了开发旅游资源，欲修建一条连接风景点P和居民区O的公路，点P所在的山坡面与山脚所在水平面α所成的二面角为(0°＜＜90°)，且sin＝，点P到平面α的距离PH＝0.4(km)．沿山脚原有一段笔直的公路AB可供利用．从点O到山脚修路的造价为a万元/km，原有公路改建费用为万元/km．当山坡上公路长度为lkm(1≤l≤2)时，其造价为(l²＋1)a万元．已知OA⊥AB，PB⊥AB，AB＝1.5(km)，OA＝(km)．

(Ⅰ)在AB上求一点D，使沿折线PDAO修建公路的总造价最小；

(Ⅱ)对于(Ⅰ)中得到的点D，在DA上求一点E，使沿折线PDEO修建公路的总造价最小．

(Ⅲ)在AB上是否存在两个不同的点，，使沿折线修建公路的总造价小于(Ⅱ)中得到的最小总造价，证明你的结论．

如图，在多面体ABCDE中，底面△ABC为等腰直角三角形，且∠ACB＝90°，侧面BCDE是棱形，O点是BC的中点，EO⊥平面ABC．

(1)求证：平面ACD⊥平面BCDE；

(2)求平面ABE与平面ADE所成锐角的余弦值．