设数列{a_n}的前n项和为S_n，已知S_n＝2a_n－2ⁿ⁺¹(n∈N*)．

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)设，数列{b_n}的前n项和为B_n，若存在整数m，使对任意n∈N*且n≥2，都有成立，求m的最大值；

(Ⅲ)令，数列{c_n}的前n项和为T_n，求证：当n∈N*且n≥2时，．

设向量a＝(x＋1，y)，b＝(x－1，y)，点P(x，y)为动点，已知|a|＋|b|＝4．

(Ⅰ)求点P的轨迹方程；

(Ⅱ)设点P的轨迹与x轴负半轴交于点A，过点F(1，0)的直线交点P的轨迹于B、C两点，试推断△ABC的面积是否存在最大值？若存在，求其最大值；若不存在，请说明理由．

如图，某化工集团在一条河流的上、下游分别建有甲、乙两家化工厂，其中甲厂每天向河道内排放污水2万m³，每天流过甲厂的河水流量是500万m³(含甲厂排放的污水)；乙厂每天向河道内排放污水1.4万m³，每天流过乙厂的河水流量是700万m³(含乙厂排放的污水)．由于两厂之间有一条支流的作用，使得甲厂排放的污水在流到乙厂时，有20％可自然净化．假设工厂排放的污水能迅速与河水混合，且甲厂上游及支流均无污水排放．根据环保部门的要求，整个河流中污水含量不能超过0.2％，为此，甲、乙两个工厂都必须各自处理一部分污水．

(Ⅰ)设甲、乙两个化工厂每天各自处理的污水分别为x、y万m³，试根据环保部门的要求写出x、y所满足的所有条件；

(Ⅱ)已知甲厂处理污水的成本是1200元/万m³，乙厂处理污水的成本是1000元/万m³，在满足环保部门要求的条件下，甲、乙两个化工厂每天应分别各自处理污水多少万m³，才能使这两个工厂处理污水的总费用最小？最小总费用是多少元？

如图，四边形ABCD是边长为2的正方形，△ABE为等腰三角形，AE＝BE，平面ABCD⊥平面ABE，点F在CE上，且BF⊥平面ACE．

(Ⅰ)判断平面ADE与平面BCE是否垂直，并说明理由；

(Ⅱ)求点D到平面ACE的距离．

甲、乙两名射击运动员进行射击选拔比赛，已知甲、乙两运动员射击的环数稳定在6，7，8，9，10环，其射击比赛成绩的分布列如下：

甲运动员：

乙运动员：

(Ⅰ)若甲、乙两运动员各射击一次，求同时击中9环以上(含9环)的概率；

(Ⅱ)若从甲、乙两运动员中只能挑选一名参加某项国际比赛，你认为让谁参加比赛较合适？并说明理由．

设角A，B，C为△ABC的三个内角．

(Ⅰ)若，求角A的大小；

(Ⅱ)设，求当A为何值时，f(A)取极大值，并求其极大值．

我们用部分自然数构造如下的数表：用a_ij(i≤j)表示第i行第j个数(i、j为正整数)，使a_ij＝a_ii＝i；每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外，如图)，设第n(n为正整数)行中各数之和为B．

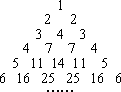
(Ⅰ)试写出b₂－2b₁，b₃－2b₂，b₄－2b₃，b₅－2b₄，并推测b_n+1和b_n的关系(无需证明)；

(Ⅱ)证明数列{b_n＋2}是等比数列，并求数列{b_n}的通项公式b_n；

(Ⅲ)数列{b_n}中是否存在不同的三项b_p，b_q，b_r(p，q，r为正整数)恰好成等差数列？若存在求出p，q，r的关系；若不存在，请说明理由．

已知函数f(x)＝x³－ax²－3x

(Ⅰ)若x＝3是f(x)的极值点，求f(x)在x∈[1，a]上的最小值和最大值；

(Ⅱ)若f(x)在x∈[1，＋∞)上是增函数，求实数a的取值范围．

某厂家拟在2009年举行促销活动，经调查测算，该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(m≥0)满足x＝3－(k为常数)，如果不搞促销活动，则该产品的年销售量只能是1万件．已知2009年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)．

(Ⅰ)将2009年该产品的利润y万元表示为年促销费用m万元的函数；

(Ⅱ)该厂家2009年的促销费用投入多少万元时，厂家的利润最大？

如图，函数y＝2cos(ωx＋)(x∈R，0≤≤)的图象与y轴相交于点(0，)，且该函数的最小正周期为π．

(Ⅰ)求和ω的值；

(Ⅱ)已知点，点P是该函数图象上一点，点Q(x₀，y₀)是PA的中点，当，时，求x₀的值．