已知f(x)＝lnx，g(x)＝x²＋mx＋(m＜0)，直线l与函数f(x)、g(x)的图像都相切，且与函数f(x)的图像的切点的横坐标为1．

(Ⅰ)求直线l的方程及m的值；

(Ⅱ)若h(x)＝f(x＋1)－(x)，求函数h(x)的最大值；

(Ⅲ)求证：对任意正整数n，总有．

设数列{a_n}的前n项和为S_n，点 (n∈N*)均在函数y＝3x－2的图象上

(1)求数列{a_n}的通项公式；

(2)设，T_n是数列{b_n}的前n项和，求使得对所有n∈N*都成立的最小正整数m．

已知动点P(x，y)(y≥0)到定点F(0，1)的距离和它到直线y＝－1的距离相等，记点P的轨迹为曲线C．

(1)求曲线C的方程；

(2)设圆M过点A(0，2)，且圆心M(a，b)在曲线C上，若圆M与x轴的交点分别为E(x₁，0)、G(x₂，0)，求线段EG的长度．

如下图所示，现有A、B、C、D四个海岛，已知B在A的正北方向5海里处，C在A的东偏北30°方向，又在D的东北方向，且B、C相距7海里，求C岛分别到A、D两岛的距离．

已知函数f(x)＝x³＋ax²＋bx＋5，若x＝－2时，f(x)有极值，且曲线y＝f(x)在点x＝1处的切线斜率为3，

(1)求函数f(x)的解析式；

(2)判断当x＝－2时，f(x)是取到极大值还是极小值，说明理由．

建造一个容积为8 m³，深为2 m的长方体无盖水池，如果池底的造价为每平方米120元，池壁的造价为每平方米80元，

(1)设池底的长为x m，试把水池的总造价S表示成关于x的函数；

(2)如何设计池底的长和宽，才能使总造价S最低，求出该最低造价．

已知：函数f(x)＝x²＋1，且g(x)＝f[f(x)]，G(x)＝g(x)－λf(x)，试问：是否存在实数λ，使得G(x)在(－∞，－1]上为减函数，并且在(－1，0)上为增函数？

在经济学中，函数f(x)的边际函数为Mf(x)，定义为Mf(x)＝f(x＋1)－f(x)，某公司每月最多生产100台报警系统装置．生产x台的收入函数为R(x)＝3000x－20x²(单位元)，其成本函数为C(x)＝500x＋4000(单位元)，利润的等于收入与成本之差．

①求出利润函数p(x)及其边际利润函数Mp(x)；

②求出的利润函数p(x)及其边际利润函数Mp(x)是否具有相同的最大值；

③你认为本题中边际利润函数Mp(x)最大值的实际意义．

已知：＝(cosx，2sinx)，＝(2cosx，－sinx)，f(x)＝·．

(Ⅰ)求f(－π)的值；

(Ⅱ)当x∈[0，]时，求g(x)＝f(x)＋sin2x的最大值和最小值．

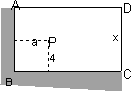
如图，周长为16米的篱笆借助一个墙角围成一个矩形ABCD，在矩形内的一点P处是一棵树，树距离两墙分别为a、4米(0＜a＜12)；若将此树围进去，又使围成的面积最大，如何围法，并求最大面积．