
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(陕西卷) 题型:044
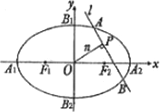
如图,椭圆C:![]() =1的顶点为A1,A2,B1,B2,焦点为F1,F2,|A1B1|=
=1的顶点为A1,A2,B1,B2,焦点为F1,F2,|A1B1|=![]() ,
,![]() =2
=2![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设n是过原点的直线,l是与n垂直相交于P点、与椭圆相交于A,B两点的直线,|![]() |=1,是否存在上述直线l使
|=1,是否存在上述直线l使![]() ·
·![]() =1成立?若存在,求出直线l的方程;若不存在,请说明理由.
=1成立?若存在,求出直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(陕西卷) 题型:044
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行出样检查,测得身高情况的统计图如下:

(Ⅰ)估计该小男生的人数;
(Ⅱ)估计该校学生身高在170~185 cm之间的概率;
(Ⅲ)从样本中身高在165~180 cm之间的女生中任选2人,求至少有1人身高在170~180 cm之间的概率.
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(陕西卷) 题型:044
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2![]() ,E,F分别是AD,PC的重点
,E,F分别是AD,PC的重点

(Ⅰ)证明:PC⊥平面BEF;
(Ⅱ)求平面BEF与平面BAP夹角的大小.
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(陕西卷) 题型:044
如图,A,B是海面上位于东西方向相聚5(3+![]() )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°且与B点相距20![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?

查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(陕西卷) 题型:044
已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项;
(Ⅱ)求数列{![]() }的前n项和Sn
}的前n项和Sn
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(安徽卷) 题型:044
品酒师需定期接受酒味鉴别功能测试,一般通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这成为一轮测试,根据一轮测试中的两次排序的偏离程度的高低为其评分.
现设n=4,分别以a1,a2,a3,a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1-a1|+|2-a2|+|3-a3|+|4-a4|则X是对两次排序的偏离程度的一种描述.
(Ⅰ)写出X的可能值集合;
(Ⅱ)假设a1a2a3a4等可能地为1.2.3.4的各种排列,求X的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中都有X≤2,
(ⅰ)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ⅱ)你认为该品酒师的酒味鉴别功能如何?说明理由.
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(安徽卷) 题型:044
设数列a1,a2,a3,a4……an+1中每一项都不为0证明,|an|为等差数列的充分必要条件是:对任何n∈N,都有![]() +
+![]() +…+
+…+![]()
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(安徽卷) 题型:044
已知椭圆E经过点A(2.,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率c=![]()
(Ⅰ)求椭圆E的方程;
(Ⅱ)求∠F1AF2的角平分线所在直线l的方程
(Ⅲ)在椭圆E上是否存在关于直线l对称的相交两点?若存在,请找出,若不存在,说明理由.
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(安徽卷) 题型:044
如图,在多面体ABCDEF中,四边形ABCD是正方形,EF∥AB,EF⊥FB,AB=2EF,∠BFC=90°,BF⊥FC,H为BC的中点.

(Ⅰ)求证:FH∥平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求二面角B-DE-C的大小
查看答案和解析>>
科目: 来源:2010年普通高等学校招生全国统一考试、理科数学(安徽卷) 题型:044
设a为实数,函数f(x)=c2-2x+2a,x∈R.
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当a>ln2-1且x>0时,c2>x2-2ax+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com