在△ABC中，a，b，c分别为角A，B，C所对的边，已知a²－(b－c)²＝bc．

(1)求角A；

(2)若BC＝2，角B为x，△ABC的周长为y，求y＝f(x)的最大值．

设曲线C：f(x)＝x³－ax＋b(a，b∈R)

(1)若函数g(x)＝lnx－[(x)＋a]－2x存在单调递减区间，求a的取值范围((x)为f(x)的导函数)

(2)若过曲线C外的点A(1，0)作曲线C的切线恰有三条，求a，b满足的关系式．

如图，斜率为1的直线l过抛物线Ω：y²＝2px(p＞0)的焦点F，与抛物线交于两点A，B．

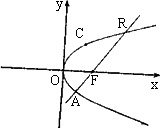
(1)若|AB|＝8，求抛物线Ω的方程；

(2)设C为抛物线弧AB上的动点(不包括A，B两点)，求△ABC的面积S的最大值；

(3)设P是抛物线Ω上异于A，B的任意一点，直线PA，PB分别交抛物线的准线于M，N两点，证明M，N两点的纵坐标之积为定值(仅与p有关)

如图所示，平面PAD⊥平面ABCD，ABCD为正方形，PA⊥AD，且PA＝AD＝2，E，F，G分别是线段PA，PD，CD的中点．

(1)求证：BC∥平面EFG；

(2)求三棱锥E－AFG的体积．

袋内装有6个球，每个球上都记有从1到6的一个号码，设号码为n的球重n²－6n＋12克，这些球等可能地从袋里取出(不受重量、号码的影响)．

(1)如果任意取出1球，求其重量大于号码数的概率；

(2)如果不放回地任意取出2球，求它们重量相等的概率．

已知向量a＝(cosx，sinx)，b＝(－sin，－cos)，其中x∈[，π]．

(1)若|a＋b|＝，求x的值；

(2)函数f(x)＝a·b＋|a＋b|²，若c＞f(x)恒成立，求实数c的取值范围．

已知数列{a_n}满a₁＝1，任意n∈N^*，有a₁＋3a₂＋5a₃＋…＋(2n－1)a_n＝pn(p为常数)

(1)求p的值及数列{a_n}的通项公式；

(2)令b_n＝a_na_n+1(n∈N^*)，求数列{b_n}的前n项和S_n．

抛物线D以双曲线C：8y²－8x²＝1的焦点F(0，c)，(c＞0)为焦点．

(1)求抛物线D的标准方程；

(2)过直线l：y＝x－1上的动点P作抛物线D的两条切线，切点为A，B．求证：直线AB过定点Q，并求出Q的坐标；

(3)在(2)的条件下，若直线PQ交抛物线D于M，N两点，求证：|PM|·|QN|＝|QM|·|PN|

已知函数f(x)＝ax(a∈R)，g(x)＝lnx－1．

(1)若函数h(x)＝g(x)＋1－f(x)－2x存在单调递减区间，求a的取值范围；

(2)当a＞0时，试讨论这两个函数图象的交点个数．

已知各项均为正数的数列{a_n}的前n项和S_n满足S₁＞1，且6S_n＝(a_n＋1)(a_n＋2)，n∈N^*．

(1)求数列{a_n}的通项公式；

(2)设数列{b_n}满足a_n(－1)＝1，记T_n为数列{b_n}的前n项和，求证：2T_n＋1＜log₂(2_n＋3)．