为了考察冰川的融化状况，一支科考队在某冰川上相距8 km的A，B两点各建一个考察基地．视冰川面为平面形，以过A，B两点的直线为x轴，线段AB的的垂直平分线为y轴建立平面直角坐标系(如图)在直线x＝2的右侧，考察范围为到点B的距离不超过km区域；在直线x＝2的左侧，考察范围为到A，B两点的距离之和不超过km区域．

(Ⅰ)求考察区域边界曲线的方程；

(Ⅱ)如图所示，设线段P₁P₂，P₂P₃是冰川的部分边界线(不考虑其他边界线)，当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0.2 km，以后每年移动的距离为前一年的2倍，求冰川边界线移动到考察区域所需的最短时间．

如图所示，在正方体ABCD－A₁B₁C₁D₁中，E是棱DD₁的中点．

(Ⅰ)求直线BE的平面ABB₁A₁所成的角的正弦值；

(Ⅱ)在棱C₁D₁上是否存在一点F，使B₁F∥平面A、BE？证明你的结论．

如图是某城市通过抽样得到的居民某年的月均用水量(单位：吨)的频率分布直方图

(Ⅰ)求直方图中x的值

(Ⅱ)若将频率视为概率，从这个城市随机抽取3位居民(看作有放回的抽样)，求月均用水量在3至4吨的居民数X的分布列和数学期望．

已知函数f(x)＝sin2x－2sin²x．

(Ⅰ)求函数f(x)的最大值；

(Ⅱ)求函数f(x)的零点的集合．

在平面直角坐标系xOy中，点B与点A(－1，1)关于原点O对称，P是动点，且直线AP与BP的斜率之积等于－

(Ⅰ)求动点P的轨迹方程；

(Ⅱ)设直线AP和BP分别与直线x＝3交于点M，N，问：是否存在点P使得△PAB与△PMN的面积相等？若存在，求出点P的坐标；若不存在，说明理由．

已知函数f(x)＝In(1＋x)－x＋x²(k≥0)．

(Ⅰ)当k＝2时，求曲线y＝f(x)在点(1，f(1))处的切线方程；

(Ⅱ)求f(x)的单调区间．

某同学参加3门课程的考试．假设该同学第一门课程取得优秀成绩的概率为，第二、第三门课程取得优秀成绩的概率分别为p，q(p＜q)，且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为

(Ⅰ)求该生至少有1门课程取得优秀成绩的概率；

(Ⅱ)求p，q的值；

(Ⅲ)求数学期望Eξ．

如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，AB＝，CE＝EF＝1．

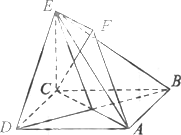
(Ⅰ)求证：AF∥平面BDE；

(Ⅱ)求证：CF⊥平面BDE；

(Ⅲ)求二面角ABED的大小．

已知函数f(x)＝2cos2x＋sin²x－4cosx．

(Ⅰ)求f＝()的值；

(Ⅱ)求f(x)的最大值和最小值．

已知集合S_n＝{X|X＝(x₁，x₂，…，x_n)，x₁∈{0，1}，i＝{1，2，…，n}(n≥2)对于A＝(a₁，a₂，…a_n)，B＝(b₁，b₂，…b_n)∈S_n，定义A与B的差为A－B＝(|a₁－b₁|，|a₂－b₂||，…|a_n－b_n|)；A与B之间的距离为d(A，B)＝|a₁－b₁|

(Ⅰ)当n＝5时，设A＝(0，1，0，0，1)，B＝(1，1，1，0，0)，求A－B，d(A，B)；

(Ⅱ)证明：A，B，C∈S_n，有A－B∈S_n，且d(A－C，B－C)＝d(A，B)；

(Ⅲ)证明：A，B，C∈S_n，d(A，B)，d(A，C)，d(B，C)三个数中至少有一个是偶数